题目内容
7.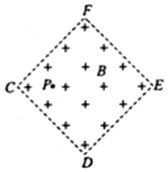 如图所示,在边长为L的正方形区域内存在垂直纸面向里的匀强磁场,其磁感应强度大小为B,在正方形对角线CE上有一点P,其到CF、CD距离均为$\frac{L}{4}$,且在P点处有一个发射正离子的装置,能连续不断地向纸面内的各方向均匀发射出速率不同的正离子.已知离子的质量为m,电荷量为q,不计离子重力及离子间相互作用力.( )
如图所示,在边长为L的正方形区域内存在垂直纸面向里的匀强磁场,其磁感应强度大小为B,在正方形对角线CE上有一点P,其到CF、CD距离均为$\frac{L}{4}$,且在P点处有一个发射正离子的装置,能连续不断地向纸面内的各方向均匀发射出速率不同的正离子.已知离子的质量为m,电荷量为q,不计离子重力及离子间相互作用力.( )| A. | 速率为0<V<$\frac{BqL}{8m}$ 范围内的 所有正离子均不能射出正方形区域 | |
| B. | 速率为0<V<$\frac{BqL}{4m}$范围内的 所有正离子均不能射出正方形区域 | |
| C. | 速率V=$\frac{BqL}{2m}$的所有正离子中能打在DE边上的离子数是其总数的$\frac{1}{6}$ | |
| D. | 速率V=$\frac{BqL}{2m}$的所有正离子中能打在DE边上的离子数是其总数的$\frac{1}{12}$ |
分析 本题分两种情况:第一是A和B考察的是要使离子不射出磁场时,最大的速度,由周边磁场及半径公式,显然是以P到CF和CD的距离为直径的圆是最大速度的轨迹.第二是当速度为某一确定值时,求打在DE上离子的总数点离子数的几分之一,显然要先分析能打在四边上离子的范围,那么打在DE上范围占四边上范围总数的几分之一,就是打在DE上离子总数的几分之一.
解答 解:AB、由于带电离子从P点以大小不同、方向也不同的速度向各个方向入射,则轨迹圆心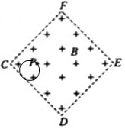
难以确定显然在向各个方向入射的离子中要使离子不从任何边界射出,则带电离子的最大半
径的轨迹如图所示,即2rmax=$\frac{1}{4}L$,由洛仑兹力提供向心力qvmaxB=m$\frac{{{v}_{max}}^{2}}{{r}_{max}}$.解得vmax=$\frac{BqL}{8m}$,
即只要小于该速度的离子均在磁场区域内做完整的匀速圆周运动,所以选项A正确,选项B错误.
CD、当粒子的速度为v=$\frac{BqL}{2m}$时,由上述半径公式可得:该离子做匀速圆周运动的半径r=$\frac{L}{2}$,
由周边磁场区域的特征,只要能穿过CD边,即轨迹与CD相切打在DE的G点,如图所示:
△POK中设CA=x,由勾股定理,(x-$\frac{1}{4}L$)2+(r-$\frac{1}{4}L$)2=r2 解得x=$\frac{\sqrt{3}+1}{4}L$.设打在DE上的
点M(打在DE上最低点)到D的距离为y,则在△OHG中由勾股定理:(L-x)2+(r-y)2=r2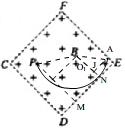

代入解得:y=$\frac{2L-\sqrt{6\sqrt{3}-8}}{4}$.当离子的轨迹与DE相切时,是打在DE上的最高点,与DE相切于N点,
打在EF上A点,如图所示,设相切点N与D点的距离为z,在△PO1Q中(z-$\frac{1}{4}L$)2+($\frac{3}{4}L-\frac{1}{2}L$)2=r2,解得:
z=$\frac{4-\sqrt{3}}{4}L$,打在DE上的范围△s=z-y=$\frac{2+\sqrt{6\sqrt{3}-8}-\sqrt{3}}{4}$在△O1AJ中,设NE=a,据勾股定理:
(L-z)2+(r-a)2=r2 解得a=$\frac{2-\sqrt{24-10\sqrt{3}}}{4}$,经分析打在正方形四边的范围有△S=CF+CAGN+AF=
L+x+y-z+L-a=$\frac{1}{12}△s$,这样打在DE上的粒子点总离子数的$\frac{1}{12}$,所以选项C错误,选项D正确.
故选:AD
点评 本题的难点在于从P点发出的离子的速度大小和方向均不同,所以需要考虑的因素比较多:①半径大小决定着轨迹的平缓程度,②速度方向也决定着有可能与周边边界的情况.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案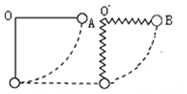 如图所示,分别用质量不计不能伸长的细线与弹簧分别吊质量相同的小球A、B,将两球拉开使细线与弹簧都在水平方向上,且高度相同,而后由静止放开A、B两球,两球在运动中空气阻力不计,到最低点时两球在同一水平面上,则两球在最低点时的速度( )
如图所示,分别用质量不计不能伸长的细线与弹簧分别吊质量相同的小球A、B,将两球拉开使细线与弹簧都在水平方向上,且高度相同,而后由静止放开A、B两球,两球在运动中空气阻力不计,到最低点时两球在同一水平面上,则两球在最低点时的速度( )| A. | A、B球的速度大小相等 | B. | A球的速度大 | ||
| C. | B球的速度大 | D. | 无法判定 |
| A. | 周期为4π$\sqrt{\frac{2R}{g}}$ | B. | 加速度为$\frac{g}{2}$ | C. | 动能为$\frac{mgR}{8}$ | D. | 速度为$\sqrt{2gR}$ |
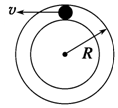 如图所示,有一个半径为R的光滑圆轨道,现给小球一个初速度,使小球在竖直面内做圆周运动,则关于小球在过最高点的速度v,下列叙述中正确的是( )
如图所示,有一个半径为R的光滑圆轨道,现给小球一个初速度,使小球在竖直面内做圆周运动,则关于小球在过最高点的速度v,下列叙述中正确的是( )| A. | v的极小值为$\sqrt{gR}$ | |
| B. | v由零逐渐增大,轨道对球的弹力逐渐增大 | |
| C. | 当v由$\sqrt{gR}$值逐渐增大时,轨道对小球的弹力也逐渐增大 | |
| D. | 当v由$\sqrt{gR}$值逐渐减小时,轨道对小球的弹力逐渐增大 |
| A. | 线速度方向时刻改变 | B. | 线速度大小时刻改变 | ||
| C. | 周期不变 | D. | 向心力指向圆心 |
| A. | 行星b的第一宇宙速度与地球相同 | |
| B. | 行星b绕恒星a运行的角速度大于地球绕太阳运行的角速度 | |
| C. | 如果将物体从地球搬到行星b上,其重力是在地球上重力的$\frac{16}{9}$ | |
| D. | 行星b与恒星a的距离是日地距离的$\sqrt{\frac{2}{73}}$倍 |
| A. | 如果物体的动能有变化,其速度也一定变化 | |
| B. | 如果物体的速度有变化,其动能也一定变化 | |
| C. | 如果合外力对物体做负功,其动能就一定变化 | |
| D. | 如果物体的动能没有变化,就一定没有外力对物体做功 |
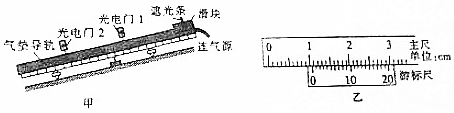 为了验证机械能守恒定律,某学生想到用气垫导轨和光电门及质量为m的小车来进行实验,如图甲所示,他将气垫导轨的一段用木块垫高,使导轨有一个倾角,将小车从导轨上端释放,光电门自动记录小车经过上、下光电门时车上挡光时间t1、t2,再用游标卡尺测得挡光片宽度d,则
为了验证机械能守恒定律,某学生想到用气垫导轨和光电门及质量为m的小车来进行实验,如图甲所示,他将气垫导轨的一段用木块垫高,使导轨有一个倾角,将小车从导轨上端释放,光电门自动记录小车经过上、下光电门时车上挡光时间t1、t2,再用游标卡尺测得挡光片宽度d,则