��Ŀ����
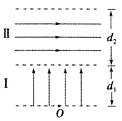
����Ŀ����ͼ��һ�̶�����ֱ������һ��һС����ͬ��ԲͲ��ɣ���ԲͲ�и���һ����������֪�����������Ϊm1=2.50kg��������Ϊs1=80.0cm2 �� С����������Ϊm2=1.50kg��������Ϊs2=40.0cm2 �� �������ø���������ӣ���ౣ��Ϊl=40.0cm�������������ѹǿΪp=1.00��105Pa���¶�ΪT=303K����ʼʱ��������ԲͲ�ײ���� ![]() ������������������¶�ΪT1=495K���������������¶Ȼ����½��������������ƣ����������������ױ�֮���Ħ�����������ٶȴ�Сgȡ10m/s2 �� ��
������������������¶�ΪT1=495K���������������¶Ȼ����½��������������ƣ����������������ױ�֮���Ħ�����������ٶȴ�Сgȡ10m/s2 �� ��
��1���ڴ�������ԲͲ�ײ��Ӵ�ǰ��˲�䣬���ڷ��������¶�
��2�����ڷ�յ��������������ﵽ��ƽ��ʱ�����ڷ�������ѹǿ��
���𰸡�
��1��
�⣺��������ԲͲ�ײ��Ӵ�ǰ���巢����ѹ�仯��
�����״̬������V1=��l�� ![]() ��s2+
��s2+ ![]() s1=��40��
s1=��40�� ![]() ����40+
����40+ ![]() ��80=2400cm3��
��80=2400cm3��
T1=495K��V2=s2l=40��40=1600cm3��
�ɸ������˶��ɵã� ![]() =
= ![]() ������
������ ![]() =
= ![]() ����ã�T2=330K
����ã�T2=330K
��2��
�⣺��������ԲͲ�ײ��Ӵ��������������������������¶���ȹ��������巢�����ݱ仯��
������ո����ԲͲ�ײ��Ӵ�ʱ����ƽ�������ã�pS1+p2S2+��m1+m2��g=p2S1+pS2��
�������ݽ�ã�p2=1.1��105Pa��
T2=330K��T3=T=303K��
�ɲ������ɵã� ![]() =
= ![]() ��
��
���� ![]() =
= ![]() ��
��
��ã�p3=1.01��105Pa
����������1�����巢����ѹ�仯������������������״̬������Ӧ�ø������˶��ɿ������������¶ȣ���2���������������ݱ仯��Ӧ�ò������ɿ�����������ѹǿ��