��Ŀ����
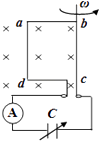
����Ŀ����ͼ��ʾ����һ�̶��Ĺ⻬��Եˮƽƽ̨��ƽ̨�Ҷ�B��ˮƽ���ʹ�ƽ����ӣ����ʹ���L=4m��һ����Ϊm=0.5kg��������Ϊq=+2��10��3C�Ļ������ˮƽƽ̨�ϣ�ƽ̨����һ�����ʵ�����˹̶����Ҷ��뻬��Ӵ��������ӣ��ֽ������A���ɾ�ֹ�ͷţ����Ҵ��ʹ�����ʱ����ǡ�ܵ��ﴫ�ʹ��Ҷ�C�㣮��֪����ʼ���ڵ������ڣ����鵽��B��ǰ���뵯����ȫ���룬�����봫�ʹ���Ķ�Ħ������Ϊ��=0.20��gȡl0m/s2 �� ��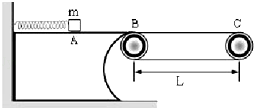
��1�����鵽��B��ʱ���ٶ�vB�͵��ɴ�������������EP��
��2�������ʹ���5m/s���ٶ���˳ʱ�뷽������ת���������B��C�Ĺ����У�Ħ�����ȶ��٣�
��3������BC֮�����ˮƽ�������ǿ�糡E=1��103N/C�����ʹ���1m/s���ٶ���˳ʱ�뷽������ת��������ڶ��ι�B��ʱ�ٶȴ�СΪ���
���𰸡�
��1��
�⣺������ͷ����˶���B�㣬�������غ�ã�
![]() ����
����
��B��C���ɶ��ܶ����ã� ![]() ����
����
�����٢���ʽ���������ݽ�ã�vB=4m/s
Ep=2J
��2��
�⣺���ٵ�5m/s���봫�ʹ�һ�������˶������ٹ��̣�����ţ�ٵڶ����ɵã�a= ![]() ��
��
����ʱ��Ϊ�� ![]() ��
��
������ٵ�λ��Ϊ�� ![]()
��Ħ������Ϊ��Q=��mg��vt1��x1��=0.25J
��3��
�⣺��B�����Ҽ��ٵ�1m/s�����ݶ��ܶ����ã� ![]()
�������ݽ�ã�x2=1.25m
��1m/s����Ϊ0�Ĺ����У����ݶ��ܶ����ã� ![]() ��
��
�������ݽ�ã�x3=0.25m��
��������B�����ݶ��ܶ����ã� ![]() ��
��
�������ݽ�ã� ![]()
����������1�����ݶ��ܶ�������ϻ�����C����ٶ�Ϊ�㣬���������B����ٶȣ����������غ�������ɴ������������ܣ���2�����黬�ϴ��ʹ����������˶������ٶ��봫�ʹ��ٶ����ʱһ�����٣�����ţ�ٵڶ����ɽ���˶�ѧ������ʽ������λ�ƣ��������Ħ�����ȣ���3����B�����Ҽ��ٵ�1m/s�����ݶ��ܶ�����ʽ����1m/s����Ϊ0�Ĺ����У����ݶ��ܶ�����ʽ���ٶԻ�������B�����ݶ��ܶ�����ʽ������������⼴�ɣ�
�����㾫����ͨ��������ù��ܹ�ϵ�����յ�ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1�����Խ����⣮