��Ŀ����
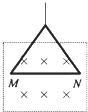
����Ŀ����ͼ��ʾ���̶���ͬһ����ֱ���ϵ�A��B���������������ֵ�ɵĵ��ɣ�������ֱ�Ϊ+Q�ͩ�Q��A��B���Ϊ2d��MN����ֱ���õĹ⻬��Եϸ�ˣ�����һ������ϸ�˵Ĵ���С��p��������Ϊm�������Ϊ+q������Ϊ���ɣ���Ӱ��糡�ķֲ������ֽ�С��P�������A�ȸߵ�C���ɾ�ֹ��ʼ�ͷţ�С��P�����˶�����C�����Ϊd��O��ʱ���ٶ�Ϊv����֪MN��AB֮��ľ���Ϊd������������Ϊk���������ٶ�Ϊg����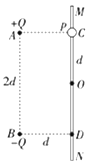
��1��C��O��ĵ��Ʋ�UCO��
��2��С��P��O��ʱ�ļ��ٶȴ�С�Լ�С��P���������B�ȸߵ�D��ʱ���ٶȴ�С��
���𰸡�
��1��
�⣺С��p��C�˶���O�Ĺ��̣��ɶ��ܶ���
��mgd+qUCO= ![]() mv2��0��
mv2��0��
����UCO= ![]() ��
��
��2��
�⣺С��p����O��ʱ������ͼ
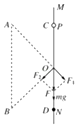
�ɿ��ض��ɵ�F1=F2=k ![]()
���ǵĺ���Ϊ
F=F1cos 45��+F2cos 45��=Eq��
����O�㴦�ĵ糡ǿ��E�T ![]() ����
����
��ţ�ٵڶ����ɵã�mg+qE=ma��
����a=g+ ![]() ��
��
С��p��O�˶���D�Ĺ��̣��ɶ��ܶ�����
mgd+qUOD= ![]() m
m ![]() ��
�� ![]() mv2��
mv2��
�ɵ糡�ص��֪UCO=UOD��
�����٢ߢ���vD= ![]() v
v
����������1����C��O�����ö��ܶ��������C��O��ĵ��Ʋ�����C��D��ĵ��Ʋ�UCD �� ��2���ɵ��ɵij�ǿ��ʽ���ƽ���ı��ζ������O��ĵ糡ǿ�ȣ��ɵ糡�ĶԳ���֪��UOD=UCO �� С���O��D�ɶ��ܶ������
�����㾫����������Ҫ�����˶��ܶ������ۺ�Ӧ�õ����֪ʶ�㣬��Ҫ����Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ�����ȷ�����⣮

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�