题目内容
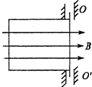 如图所示,边长为a的单匝正方形线圈在磁感强度为B的匀强磁场中,以OO′边为轴匀速转动,角速度为ω,转轴与磁场方向垂直,线圈电阻为R,求:
如图所示,边长为a的单匝正方形线圈在磁感强度为B的匀强磁场中,以OO′边为轴匀速转动,角速度为ω,转轴与磁场方向垂直,线圈电阻为R,求:(1)交流电的变化规律表达式;
(2)线圈从图示位置转过
| π |
| 2 |
(3)线圈从图示位置转过
| π |
| 2 |
分析:线框在匀强磁场中匀速转动,产生正弦式交变电流,根据规律可列出感应电动势的瞬时表达式,
线圈产生的热量,根据焦耳定律Q=I2Rt求解热量,
通过线圈某截面的电量用q=It求解.
线圈产生的热量,根据焦耳定律Q=I2Rt求解热量,
通过线圈某截面的电量用q=It求解.
解答:解:线圈中产生的热量需要从转动过程中交流电的有效值考虑;通过线圈截面的电量需从交流电的平均值考虑.
(1)因为最大值为Em=Bωa2,而线圈中垂直中性面开始转动,所以表达式为
e=Bωa2cosωt
(2)线圈转动中感应电动势的峰值Em=Bωa2,感应电流的有效值为
I=
=
线圈转过
的时间t=
,所以在转动过程中产生的热量为
Q=I2Rt=
(3)线圈转过
过程中的感应电动势和感应电流的平均值分别为
=
=
,
=
=
所以,在转动过程中流过导体截面的电量为
q=It=
答:(1)交流电的变化规律表达式是e=Bωa2cosωt;
(2)线圈从图示位置转过
的过程中产生的热量是
;
(3)线圈从图示位置转过
的过程中通过线圈某截面的电量是
.
(1)因为最大值为Em=Bωa2,而线圈中垂直中性面开始转动,所以表达式为
e=Bωa2cosωt
(2)线圈转动中感应电动势的峰值Em=Bωa2,感应电流的有效值为
I=
| Im | ||
|
| Bωa2 | ||
|
线圈转过
| π |
| 2 |
| π |
| 2ω |
Q=I2Rt=
| πB2ωa4 |
| 4R |
(3)线圈转过
| π |
| 2 |
. |
| E |
| △Φ |
| △t |
| 2Ba2ω |
| π |
. |
| I |
| ||
| R |
| 2Ba2ω |
| πR |
所以,在转动过程中流过导体截面的电量为
q=It=
| Ba2 |
| R |
答:(1)交流电的变化规律表达式是e=Bωa2cosωt;
(2)线圈从图示位置转过
| π |
| 2 |
| πB2ωa4 |
| 4R |
(3)线圈从图示位置转过
| π |
| 2 |
| Ba2 |
| R |
点评:线框在匀强磁场中匀速转动,产生正弦式交变电流.而对于电表读数、求产生的热量均由交变电的有效值来确定,而涉及到耐压值时,则由最大值来确定.而通过某一电量时,则用平均值来求.

练习册系列答案
相关题目
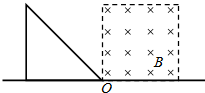 如图所示,边长为a的正方形区域内分布有垂直于纸面向里的匀强磁场,正方形的一条边刚好与x轴重合.纸面内一直角边长为a的等腰直角三角形导线框以恒定速度沿x轴正方向穿过磁场区域,在t=0时刻恰好位于图示的位置.以逆时针方向为导线框中电流的正方向,下列四幅图能够正确表示导线框中电流-位移关系(i-x)的是( )
如图所示,边长为a的正方形区域内分布有垂直于纸面向里的匀强磁场,正方形的一条边刚好与x轴重合.纸面内一直角边长为a的等腰直角三角形导线框以恒定速度沿x轴正方向穿过磁场区域,在t=0时刻恰好位于图示的位置.以逆时针方向为导线框中电流的正方向,下列四幅图能够正确表示导线框中电流-位移关系(i-x)的是( ) 如图所示,边长为a的正三角形ABC将平面分为两个区域,在三角形内区域存在垂直于纸面的匀强磁场,在三角形外区域存在三个宽度都为a、场强大小都为E、方向分别垂直于边AB、BC和AC且指向三边的匀强电场.一个质量为m、带电量为q(q>0)的粒子从AB边的垂直平分线上的P点静止释放,粒子将以一定的速度从D点射入磁场,经过磁场偏转后又从BC边的中点F射出磁场,已知P、D两点的距离为l.不计粒子重力影响.
如图所示,边长为a的正三角形ABC将平面分为两个区域,在三角形内区域存在垂直于纸面的匀强磁场,在三角形外区域存在三个宽度都为a、场强大小都为E、方向分别垂直于边AB、BC和AC且指向三边的匀强电场.一个质量为m、带电量为q(q>0)的粒子从AB边的垂直平分线上的P点静止释放,粒子将以一定的速度从D点射入磁场,经过磁场偏转后又从BC边的中点F射出磁场,已知P、D两点的距离为l.不计粒子重力影响.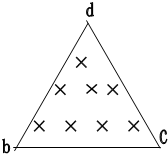 (2006?广东模拟)如图所示,边长为a的等边三角形bcd所围区域内磁感应强度为B,方向垂直纸面向内的匀强磁场,某时刻静止在b点的原子核X发生α衰变,α粒子沿bc方向射入磁场,经磁场偏转后恰好在d点沿cd方向射出.已知α粒子质量为m,电量为2e,剩余核的质量为M,衰变过程的核能全部转化为动能,求原子核X的质量MX.
(2006?广东模拟)如图所示,边长为a的等边三角形bcd所围区域内磁感应强度为B,方向垂直纸面向内的匀强磁场,某时刻静止在b点的原子核X发生α衰变,α粒子沿bc方向射入磁场,经磁场偏转后恰好在d点沿cd方向射出.已知α粒子质量为m,电量为2e,剩余核的质量为M,衰变过程的核能全部转化为动能,求原子核X的质量MX.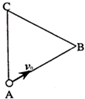 如图所示,边长为a的等边三角形ABC区域中存在垂直纸面向里的匀强磁场,AC边右侧存在竖直方向的匀强电场,场强为E,一带正电、电量为q的小球以速度v0沿AB边射入匀强磁场中恰能做匀速圆周运动,欲使带电小球能从AC边射出,匀强磁场的磁感应强度B的取值应为( )
如图所示,边长为a的等边三角形ABC区域中存在垂直纸面向里的匀强磁场,AC边右侧存在竖直方向的匀强电场,场强为E,一带正电、电量为q的小球以速度v0沿AB边射入匀强磁场中恰能做匀速圆周运动,欲使带电小球能从AC边射出,匀强磁场的磁感应强度B的取值应为( )