题目内容
 如图所示,边长为a的正三角形ABC将平面分为两个区域,在三角形内区域存在垂直于纸面的匀强磁场,在三角形外区域存在三个宽度都为a、场强大小都为E、方向分别垂直于边AB、BC和AC且指向三边的匀强电场.一个质量为m、带电量为q(q>0)的粒子从AB边的垂直平分线上的P点静止释放,粒子将以一定的速度从D点射入磁场,经过磁场偏转后又从BC边的中点F射出磁场,已知P、D两点的距离为l.不计粒子重力影响.
如图所示,边长为a的正三角形ABC将平面分为两个区域,在三角形内区域存在垂直于纸面的匀强磁场,在三角形外区域存在三个宽度都为a、场强大小都为E、方向分别垂直于边AB、BC和AC且指向三边的匀强电场.一个质量为m、带电量为q(q>0)的粒子从AB边的垂直平分线上的P点静止释放,粒子将以一定的速度从D点射入磁场,经过磁场偏转后又从BC边的中点F射出磁场,已知P、D两点的距离为l.不计粒子重力影响.(1)求粒子射入磁场的速度的大小;
(2)求磁场的磁感应强度的大小和方向;
(3)粒子的运动是否是周期性运动?如果你认为粒子做的是周期性运动,请求出运动周期;如果你认为粒子做的不是周期性运动,请说明理由.
分析:(1)粒子在电场力作用下从P点到D点做匀加速直线运动,由动能定理可以求得粒子的速度的大小;
(2)粒子从D点垂直进入磁场,从F点垂直离开磁场,由几何关系可以得知磁场的磁感应强度的大小;
(3)由于三角形是正三角形,粒子从中点D进入磁场,从中点F离开磁场,根据粒子的运动情况可知,粒子还可以沿原来的轨迹返回,最终粒子还可以到达D点,所以粒子的运动时周期性的.
(2)粒子从D点垂直进入磁场,从F点垂直离开磁场,由几何关系可以得知磁场的磁感应强度的大小;
(3)由于三角形是正三角形,粒子从中点D进入磁场,从中点F离开磁场,根据粒子的运动情况可知,粒子还可以沿原来的轨迹返回,最终粒子还可以到达D点,所以粒子的运动时周期性的.
解答:解:(1)粒子在电场力作用下从P点到D点做匀加速直线运动,设加速度为a,进入磁场的速度为υ,
由牛顿第二定律和运动学公式,有
Eq=ma
υ2-0=2al
解得v=
(2)粒子从D点沿圆弧运动到F点,圆弧的圆心为B点,所以圆弧半径R为:R=
由洛仑兹力公式和牛顿第二定律,有qvB=m
解得 B=
磁感应强度的方向垂直于纸面向外.
(3)粒子的运动是周期性运动.
设粒子从P点到D点的时间为t1,从D点到F点的时间为t2,则l=
a
T=
t2=
t=3(2t1+t2)
解得 t=(6
+π)
=11.6
.
由牛顿第二定律和运动学公式,有
Eq=ma
υ2-0=2al
解得v=
|
(2)粒子从D点沿圆弧运动到F点,圆弧的圆心为B点,所以圆弧半径R为:R=
| l |
| 2 |
由洛仑兹力公式和牛顿第二定律,有qvB=m
| v2 |
| R |
解得 B=
|
磁感应强度的方向垂直于纸面向外.
(3)粒子的运动是周期性运动.
设粒子从P点到D点的时间为t1,从D点到F点的时间为t2,则l=
| 1 |
| 2 |
| t | 2 1 |
T=
| 2πR |
| v |
t2=
| T |
| 6 |
t=3(2t1+t2)
解得 t=(6
| 2 |
|
|
点评:本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.

练习册系列答案
相关题目
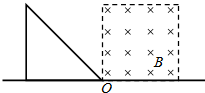 如图所示,边长为a的正方形区域内分布有垂直于纸面向里的匀强磁场,正方形的一条边刚好与x轴重合.纸面内一直角边长为a的等腰直角三角形导线框以恒定速度沿x轴正方向穿过磁场区域,在t=0时刻恰好位于图示的位置.以逆时针方向为导线框中电流的正方向,下列四幅图能够正确表示导线框中电流-位移关系(i-x)的是( )
如图所示,边长为a的正方形区域内分布有垂直于纸面向里的匀强磁场,正方形的一条边刚好与x轴重合.纸面内一直角边长为a的等腰直角三角形导线框以恒定速度沿x轴正方向穿过磁场区域,在t=0时刻恰好位于图示的位置.以逆时针方向为导线框中电流的正方向,下列四幅图能够正确表示导线框中电流-位移关系(i-x)的是( )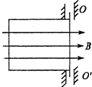 如图所示,边长为a的单匝正方形线圈在磁感强度为B的匀强磁场中,以OO′边为轴匀速转动,角速度为ω,转轴与磁场方向垂直,线圈电阻为R,求:
如图所示,边长为a的单匝正方形线圈在磁感强度为B的匀强磁场中,以OO′边为轴匀速转动,角速度为ω,转轴与磁场方向垂直,线圈电阻为R,求: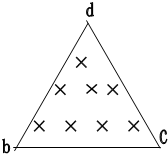 (2006?广东模拟)如图所示,边长为a的等边三角形bcd所围区域内磁感应强度为B,方向垂直纸面向内的匀强磁场,某时刻静止在b点的原子核X发生α衰变,α粒子沿bc方向射入磁场,经磁场偏转后恰好在d点沿cd方向射出.已知α粒子质量为m,电量为2e,剩余核的质量为M,衰变过程的核能全部转化为动能,求原子核X的质量MX.
(2006?广东模拟)如图所示,边长为a的等边三角形bcd所围区域内磁感应强度为B,方向垂直纸面向内的匀强磁场,某时刻静止在b点的原子核X发生α衰变,α粒子沿bc方向射入磁场,经磁场偏转后恰好在d点沿cd方向射出.已知α粒子质量为m,电量为2e,剩余核的质量为M,衰变过程的核能全部转化为动能,求原子核X的质量MX.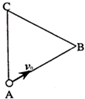 如图所示,边长为a的等边三角形ABC区域中存在垂直纸面向里的匀强磁场,AC边右侧存在竖直方向的匀强电场,场强为E,一带正电、电量为q的小球以速度v0沿AB边射入匀强磁场中恰能做匀速圆周运动,欲使带电小球能从AC边射出,匀强磁场的磁感应强度B的取值应为( )
如图所示,边长为a的等边三角形ABC区域中存在垂直纸面向里的匀强磁场,AC边右侧存在竖直方向的匀强电场,场强为E,一带正电、电量为q的小球以速度v0沿AB边射入匀强磁场中恰能做匀速圆周运动,欲使带电小球能从AC边射出,匀强磁场的磁感应强度B的取值应为( )