题目内容
（9分）如图18所示，光滑水平地面上停放着甲、乙两辆相同的平板车，一根轻绳跨过乙车的定滑轮（不计定滑轮的质量和摩擦），绳的一端与甲车相连，另一端被甲车上的人拉在手中，已知每辆车和人的质量均为30kg，两车间的距离足够远。现在人用力拉绳，两车开始相向运动，人与甲车始终保持相对静止，当乙车的速度为0.5m/s时，停止拉绳。求人在拉绳过程中做了多少功？
解：设甲、乙两车和人的质量分别为m甲、m乙和m人，停止拉绳时
甲车的速度为v甲，乙车的速度为v乙，由动量守恒定律得
（m甲+m人）v甲=m乙v乙 求得：v甲=0.25m/s （5分）
由功能关系可知，人拉绳过程做的功等于系统动能的增加量。
（4分）
甲车的速度为v甲，乙车的速度为v乙，由动量守恒定律得
（m甲+m人）v甲=m乙v乙 求得：v甲=0.25m/s （5分）
由功能关系可知，人拉绳过程做的功等于系统动能的增加量。
（4分）略
练习册系列答案
世纪百通期末金卷系列答案
相关题目
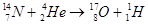。在些反应室内有“α粒子、氮原子核、质子、氧的同位素”共存，它们间常发生碰撞。设有速度为v的氮核与静止的质子发生弹性正碰，求碰撞后两个粒子的速度。已知氮核的质量mN质子的质量mH(只要求写出方程或方程组即可，不要求解方程)。
，重力加速度为g．求：
圆弧槽，圆弧槽底端的切线与A的上表面相平.现在A和C以共同速度v0冲向静止的B
