Question

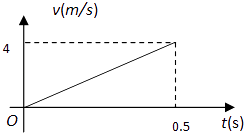
【题目】如图a所示，匀强磁场垂直于xOy平面，磁感应强度B1按图b所示规律变化（垂直于纸面向外为正）．t=0时，一比荷为 =1×105C/kg的带正电粒子从原点沿y轴正方向射入，速度大小v=5×104m/s，不计粒子重力．

（1）求带电粒子在匀强磁场中运动的轨道半径．
（2）求t= ×10﹣4s时带电粒子的坐标．
（3）保持b中磁场不变，再加一垂直于xOy平面向外的恒定匀强磁场B2 ， 其磁感应强度为0.3T，在t=0时，粒子仍以原来的速度从原点射入，求粒子回到坐标原点的时刻．

Answer 1

【答案】
（1）解：带电粒子在匀强磁场中运动，洛仑兹力提供向心力，

代入数据解得：

r=1m

答：求带电粒子在匀强磁场中运动的轨道半径为1m；

（2）解：带电粒子在磁场中运动的周期， s

在0～ s过程中，粒子运动了 ，

圆弧对应的圆心角，

在 s～ s过程中，粒子又运动了 ，

圆弧对应的圆心角，

轨迹如图a所示，根据几何关系可知，

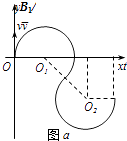
横坐标： m

纵坐标： m

带电粒子的坐标为（3.41m，﹣1.41m）

答：t= ×10﹣4s时带电粒子的坐标为[3.41m，﹣1.41m]；

（3）解：施加B2=0.3T的匀强磁场与原磁场叠加后，如图b所示，

①当 （n=0，1，2，…）时， s

②当 （n=0，1，2，…）时，

粒子运动轨迹如图c所示，则粒子回到原点的时刻为，

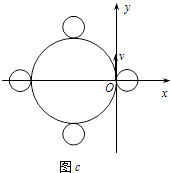
（n=0，1，2，…）

答：粒子回到坐标原点的时刻为t1=（ +2nπ）×10﹣4s，t2=2（n+1）π×10﹣4s （n=0，1，2，…）．

【解析】本题考查带电粒子在匀强电场中的运动，解题时要分析好粒子的运动轨迹，注意粒子运动的周期性，画出粒子的运动轨迹并结合几何知识求解。