题目内容
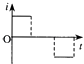
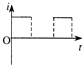
【题目】质量为0.1kg 的弹性球从空中某高度由静止开始下落,该下落过程对应的v﹣t图象如图所示.球与水平地面相碰后离开地面时的速度大小为碰撞前的 ![]() .设球受到的空气阻力大小恒为f,取g=10m/s2 , 求:
.设球受到的空气阻力大小恒为f,取g=10m/s2 , 求: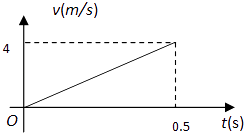
(1)弹性球受到的空气阻力f的大小;
(2)弹性球第一次碰撞后反弹的高度h.
【答案】
(1)解:设弹性球第一次下落过程中的加速度为a,由速度时间图象得:
a= ![]()
根据牛顿第二定律得:mg﹣f=ma
解得:f=0.2N
答:弹性球受到的空气阻力f的大小为0.2N;
(2)由速度时间图象可知,弹性球第一次到达地面的速度为v=4m/s
则弹性球第一次离开地面时的速度大小为v′=3m/s
离开地面后a′= ![]() =12m/s2,
=12m/s2,
根据0﹣v′2=2a′h
解得:h=0.375m
答:弹性球第一次碰撞后反弹的高度h为0.375m.
【解析】(1)首先明确速度时间图象的物理意义,斜率代表物体的加速度,然后根据牛顿第二定律求解。
(2)首先求出弹性球第一次到达地面的速度和第一次离开地面时的速度,然后根据牛顿第二定律求出加速度,最后利用速度和位移的关系求解。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目