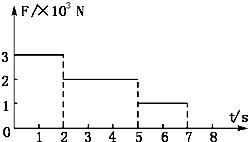��Ŀ����
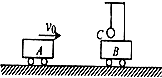
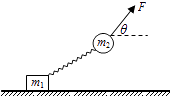
����Ŀ����ͼ1��ʾ������Ϊ1kg�Ļ��飨����Ϊ�ʵ㣩��������h=2m��A���شֲڻ��ι���Գ��ٶ�v0=4m/s��ʼ�»�����B����ٶ�Ϊ6m/s��ͨ���ֲ�ˮƽ���BC�������Ź⻬�İ�Բ����˶�����֪������ˮƽ���BC��Ķ�Ħ��������=0.10����C��O��D������ͬһ��ֱ���ϣ���ˮƽ�����BC=x���⻬��Բ����İ뾶��СΪ0.4m��g=10m/s2 �� 
��1�������A����B�˷�Ħ�����Ĺ���
��2����x=2m����չ�C��ʱ��Բ�����ѹ���Ƕ��
��3����ͼ2����ϵ�ڻ��������D���Բ�����ѹ��FD��ˮƽ�����x֮���ϵͼ��
���𰸡�
��1��
�⣺�����A����B���̣����ö��ܶ�����
mgh��Wf= ![]() mvB2��
mvB2�� ![]() mv02
mv02
��û����A����B�˷�Ħ�����Ĺ� Wf=10J
��2��
�⣺�����B����C���̣��ɶ��ܶ�������
����mgx= ![]() mvC2��
mvC2�� ![]() mvB2
mvB2
��C�㣬�Ի�������������ʽ����
FC��mg=m ![]()
��� FC=90N
��ţ�ٵ������ɣ��û���չ�C��ʱ��Բ�����ѹ�� F��C=FC=90N
��3��
�⣺�����B����D���̣��ɶ��ܶ�������
����mgx��mg2R= ![]() mvD2��
mvD2�� ![]() mvB2
mvB2
��D�㣬����������ʽ����
FD+mg=m ![]()
������ã�FD=40��5x�����������D���Բ�����ѹ��FD��ˮƽ�����x֮���ϵͼ��������ʾ��
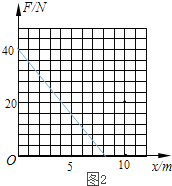
����������1�������A����B���̣����ö��ܶ�����˷�Ħ�����Ĺ�����2�������B����C���̣����ö��ܶ���������鵽��C��ʱ���ٶȣ���ţ�ٵڶ����ɡ�����������չ�C��ʱ��Բ�����ѹ������3�������B����D���̣����ö��ܶ�����ʽ���õ�ͨ������ͨ��D����ٶȣ�������������ʽ���FD��x�Ĺ�ϵʽ��������ͼ��
�����㾫����������Ҫ�����˶��ܶ������ۺ�Ӧ�õ����֪ʶ�㣬��Ҫ����Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ�����ȷ�����⣮

 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�