Question

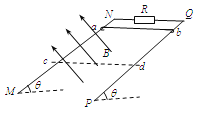
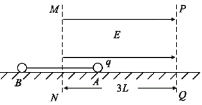
【题目】如图所示，在光滑绝缘水平面上，用长为2L的绝缘轻杆连接两个质量均为m的小球A和B，组成一个系统。其中A球带正电，电量为q。虚线MN与PQ平行且相距3L，开始时A 和B分别静止于虚线MN的两侧，虚线MN恰为AB两球连线的垂直平分线。视小球为质点， 不计轻杆的质量，在虚线MN、PQ间加上水平向右的匀强电场后，系统开始运动.若B球不带 电时，B球到达虚线PQ位置时速度大小为；若让B 球带上一定电荷，B球从图示位置向右恰能运动到虚线PQ位置，不计A、B两球间的库仑力，两球均视为点电荷。求：

（1）虚线MN与PQ之间的电势差；

（2）B 球的电性，B球所带电荷量；

(3)B球带上述电荷后，从系统开始运动到B球第二次经过虚线MN位置的时间。

Answer 1

【答案】（1） ；（2）；（3）

【解析】

(1)B球不带电时，从图示位置运动到PQ位置的过程中，以AB系统为研究对象，由动能定理有：2EqL=

根据U=Ed可知MN与PQ之间的电势差：U=E·3L

联立可得：

(2)B球带负电。令B球的带电量为qB，AB系统从开始至B球恰好到达PQ位置的过程中，由动能定理有：

可得：

(3)仅A在电场中： Eq=2ma1

可得：

a1=2g

AB系统做初速度为0，加速度为的a1匀加速直线运动，位移为L，由：，

可得：

由：，可得：

仅B在电场中：EqB=2ma3，可得：

AB系统做加速度为的a3匀减速直线运动，位移为2L，由：

可得：

则该过程的初速度：，可得：

AB都在电场中：E（q-qB）=2ma2，可得：

AB系统做加速度为的a2匀边速直线运动，位移为L，始末速度分别为v1、v2由：v2=v1+a2t2 ，可得：

根据运动的对称性，可知全过程的总时间：t=t1+2(t2+t3)，可得：