题目内容
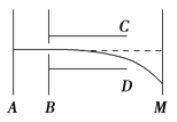
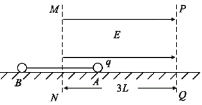
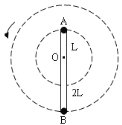
【题目】如图所示,轻杆长为 3L,杆两端分别固定质量为 m 的 A 球和质量为 3m 的 B 球,杆上距球为 L 处的O 点装在水平转轴上,杆在水平轴的带动下沿竖直平面转动,问:
(1)若 A 球运动到最高点时,A 球对杆 OA 恰好无作用力,求此时水平轴所受的力;
(2)在杆的转速逐渐增大的过程中,当杆转至竖直位置时,能否出现水平轴不受力情况?如果出现这种情况,A、B 两球的运动速度分别为多大?
【答案】(1)9mg (2)![]() ;
;![]()
【解析】
(1)设杆对B球的拉力为T,则有
mg=mLω2
T-3mg=3m2Lω2
解得
T=9mg
所以杆对轴的作用为T′=9mg.
(2)杆对两球的作用力大小相等、方向相反,轴才不受力.根据分析可知,此时A球应在下方,B球应在上方,由此得
对B球
3mg+T=3mω22L
对A球
T-mg=mω2L
解得
![]()
此时A的速度
![]()
![]()

 名校课堂系列答案
名校课堂系列答案【题目】一物理兴趣小组利用学校实验室的数字实验系统探究物体作圆周运动时向心力与角速度、半径的关系.

(1)首先,他们让一砝码做半径r为0.08m的圆周运动,数字实验系统通过测量和计算得到若干组向心力F和对应的角速度ω,如下表.请你根据表中的数据在图甲上绘出F-ω的关系图像_______.
实验序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
F/N | 2.42 | 1.90 | 1.43 | 0.97 | 0.76 | 0.50 | 0.23 | 0.06 |
ω/rad·s-1 | 28.8 | 25.7 | 22.0 | 18.0 | 15.9 | 13.0 | 8.5 | 4.3 |
(2)通过对图像的观察,兴趣小组的同学猜测F与ω2成正比.你认为,可以通过进一步的转换,通过绘出____________关系图像来确定他们的猜测是否正确.

(3)在证实了F∝ω2之后,他们将砝码做圆周运动的半径r再分别调整为0.04m、0.12m,又得到了两条F-ω图像,他们将三次实验得到的图像放在一个坐标系中,如图乙所示.通过对三条图像的比较、分析、讨论,他们得出F∝ r的结论,你认为他们的依据是_______.
(4)通过上述实验,他们得出:做圆周运动的物体受到的向心力F与角速度ω、半径r的数学关系式是F=kω2r,其中比例系数k的大小为__________,单位是________.