题目内容
【题目】如图所示，质量为m可看作质点的小球从静止开始沿斜面由A点滑到B点后，进入与斜面圆滑连接的 
竖直圆弧管道 
，管道出口为C，圆弧半径R=15cm，AB的竖直高度差h=35cm．在紧靠出口C处，有一水平放置且绕其水平轴线匀速旋转的圆筒（不计筒皮厚度），筒上开有小孔D，筒旋转时，小孔D恰好能经过出口C处．若小球射出C口时，恰好能接着穿过D孔，并且还能再从D孔向上穿出圆筒，小球返回后又先后两次向下穿过D孔而未发生碰撞．不计摩擦和空气阻力，取g=10m/s2 ， 问：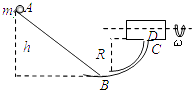
（1）小球到达C点的速为多少度vc为多少？
（2）圆筒转动的最大周期T？
（3）在圆筒以最大周期T转动的情况下，要完成上述运动圆筒的半径R′必须为多少？
【答案】
（1）
解：对小球从A→C由机械能守恒定律得：mgh=mgR+ 
代入数值解出 v0=2m/s
（2）
解：如图所示，小球向上穿出圆筒所用时间为t1
则t1= 
（k=1，2，3…）
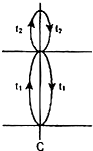
小球从离开圆筒到第二次进入圆筒所用时间为2t2．
2t2=nT （n=1，2，3…）
对小球由C竖直上抛的上升阶段，由速度公式得：
0=v0﹣g（t1+t2）
联立解得 T= 
s
当n=k=1时，Tmax=0.2s
（3）
解：对小球在圆筒内上升的阶段，由位移公式得：
2R′=v0t1﹣ 
代入数值解得 R′=0.075m
【解析】（1）对小球从A→C，运用根据机械能守恒定律求出小球到达C点的速度．（2）小球向上穿出圆筒所用时间是转动周期的奇数倍，小球从离开圆筒到第二次进入圆筒所用时间是圆筒周期的整数倍，根据竖直上抛运动的时间求出周期的通项，即可求得最大周期．（3）根据周期的表达式求出最大周期，从而求出在圆筒内竖直上升的位移，即半径的2倍，根据该关系求出圆筒的半径．
【考点精析】关于本题考查的机械能守恒及其条件和机械能综合应用，需要了解在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变；系统初态的总机械能E 1 等于末态的总机械能E 2 ，即E1 =E2；系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ，即ΔE P减 =ΔE K增；若系统只有A、
