题目内容
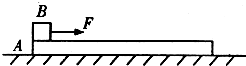
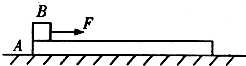 如图所示,长L=1m,质量M=1kg的木板A静止在光滑水平面上,在A的左端点有一质量也为m=1kg的木块B(可视为质点).现以水平力F=20N作用于B,使B由静止开始运动.已知B与A间的动摩擦因数=0.5,要使B恰好运动到A的右端点但不掉下来,F只能作用多长时间?(g=10m/s2)(结果可用根式表示).
如图所示,长L=1m,质量M=1kg的木板A静止在光滑水平面上,在A的左端点有一质量也为m=1kg的木块B(可视为质点).现以水平力F=20N作用于B,使B由静止开始运动.已知B与A间的动摩擦因数=0.5,要使B恰好运动到A的右端点但不掉下来,F只能作用多长时间?(g=10m/s2)(结果可用根式表示).分析:在F作用的时间t内,根据动量定理分别对两个物体列方程,得到撤去F时两物体的速度与作用时间的关系式.由平均速度与时间的乘积求出两物体相对位移大小.撤去F后,由系统的动量守恒求出两物体相对静止时共同的速度,由能量守恒列出速度与相对于位移的关系式,联立求解时间.
解答:解:在F作用的时间t内,根据动量定理得
对B:(F-μmg)t=mv1 ①
对A:μmgt=Mv2 ②
此过程中B相对于A的位移大小为S=SB-SA=
t-
t ③
要使B恰好运动到A的右端点但不掉下来时,两物体的速度相等,设为v.
对F撤去后过程,根据动量守恒定律得
mv1+Mv2=(M+m)v ④
根据能量守恒定律得
μmg(L-S)=
m
+
M
-
(M+m)v2 ⑤
联立上述五式得
t=
s
答:要使B恰好运动到A的右端点但不掉下来,F只能作用
s.
对B:(F-μmg)t=mv1 ①
对A:μmgt=Mv2 ②
此过程中B相对于A的位移大小为S=SB-SA=
| v1 |
| 2 |
| v2 |
| 2 |
要使B恰好运动到A的右端点但不掉下来时,两物体的速度相等,设为v.
对F撤去后过程,根据动量守恒定律得
mv1+Mv2=(M+m)v ④
根据能量守恒定律得
μmg(L-S)=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
联立上述五式得
t=
| ||
| 10 |
答:要使B恰好运动到A的右端点但不掉下来,F只能作用
| ||
| 10 |
点评:本题是复杂的力学综合题,寻找解题规律是关键.本题也可以采用牛顿第二定律和运动学公式综合求解.

练习册系列答案
相关题目
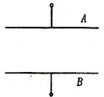 的带电小油滴,从两板左侧正央位置,以水平速度v0=10m/s射入,重力加速度g=m/s2.
的带电小油滴,从两板左侧正央位置,以水平速度v0=10m/s射入,重力加速度g=m/s2.