题目内容
12. “水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,则( )
“水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,则( )| A. | 小球运动到最低点Q时,处于失重状态 | |
| B. | 小球初速度v0越大,则在P、Q两点绳对小球的拉力差越大 | |
| C. | 当v0>√6gl时,小球一定能通过最高点P | |
| D. | 当v0<√gl时,细绳始终处于绷紧状态 |
分析 根据加速度的方向判断小球处于超重还是失重.根据牛顿第二定理,结合动能定理得出最高点和最低点拉力差的关系式,判断拉力差与初速度是否有关.根据牛顿第二定理得出最高点的最小速度,根据动能定理得出初速度的最小值.根据动能定理求出不越过四分之一圆周的最小初速度,从而判断绳子是否处于绷紧状态.
解答 解:A、小球运动到最低点Q时,加速度的方向向上,处于超重状态,故A错误.
B、设小球在P点的速度为v1,根据牛顿第二定律得:mg+F1=mv12l,解得:F1=mv12l-mg,设小球在Q点的速度为v2,根据牛顿第二定律得:F2−mg=mv22l,解得:F2=mg+mv22l,根据动能定理得:mg•2l=12mv22−12mv12,联立解得:△F=F2-F1=6mg,可知拉力差与小球的初速度无关,故B错误.
C、小球通过最高点的最小速度v=√gl,根据动能定理得:−mg•2l=12mv2−12mv02,解得初速度的最小值为:v0=√5gl,故C正确.
D、根据动能定理得,−mgl=0−12mv02,解得不越过四分之一圆周的最小速度v0=√2gl,可知当v0<√gl时,细绳始终处于绷紧状态,故D正确.
故选:CD.
点评 本题考查了动能定理、牛顿第二定律的综合运用,知道最高点和最低点向心力的来源,注意绳子绷紧要满足的条件:1、越过最高点,2、不越过四分之一圆周.

练习册系列答案
相关题目
3.物体从长为L的光滑斜面顶端开始下滑,滑到底端的速率为v,如果物体以v0=v3的初速度从斜面底端上滑,上滑时加速度与下滑时加速度大小相同且恒定,则可以达到的最大距离为( )
| A. | L3 | B. | L9 | C. | L4 | D. | √33L |
20.物体以5m/s的速度匀速通过直线上的A、B两点,所用时间为2s,现在物体从A点由静止出发,先做匀加速直线运动(加速度为a1)到某一最大速度vm,然后立即做匀减速直线运动(加速度大小为a2)至B点速度恰好减为0,所用时间仍为2s.则物体的( )
| A. | vm只能为10m/s,与a1、a2的大小无关 | |
| B. | vm可为许多值,与a1、a2的大小有关 | |
| C. | a1、a2必须满足1a1+1a2=15s2/m | |
| D. | a1、a2必须是一定的 |
7.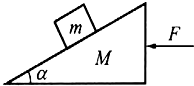 如图所示,在光滑水平而上有一质量为M的斜劈,其斜面倾角为α,一质量为m的物体放在其光滑斜面上,现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,则斜劈对物块m的弹力大小为( )
如图所示,在光滑水平而上有一质量为M的斜劈,其斜面倾角为α,一质量为m的物体放在其光滑斜面上,现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,则斜劈对物块m的弹力大小为( )
 如图所示,在光滑水平而上有一质量为M的斜劈,其斜面倾角为α,一质量为m的物体放在其光滑斜面上,现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,则斜劈对物块m的弹力大小为( )
如图所示,在光滑水平而上有一质量为M的斜劈,其斜面倾角为α,一质量为m的物体放在其光滑斜面上,现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,则斜劈对物块m的弹力大小为( )| A. | mgcosα | B. | mgcosα | C. | mF(M+m)cosα | D. | mF(M+m)sinα |
1. 有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )
有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )
 有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )
有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )| A. | 4 m,1 m | B. | -4 m,1 m | C. | 5 m,0 | D. | -5 m,1 m |
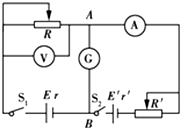 采用伏安法测量电源电动势E和内阻r时,由于电表因素带来了实验的系统误差.某研究性学习小组对此实验进行改变,设计出如图所示的测量电源电动势E和内电阻r的电路,E′是辅助电源,A、B两点间有一灵敏电流计G.
采用伏安法测量电源电动势E和内阻r时,由于电表因素带来了实验的系统误差.某研究性学习小组对此实验进行改变,设计出如图所示的测量电源电动势E和内电阻r的电路,E′是辅助电源,A、B两点间有一灵敏电流计G.