题目内容
13.质量为M的小船以速度v0行驶,船上有两个质量均为m的小孩a和b,分别静止站在船头和船尾.现小孩a沿水平方向以速率v(相对于静止水面)向前跃入水中,然后小孩b沿水平方向以同一速率v(相对于静止水面)向后跃入水中,则小孩b跃出后小船的速度方向向前(填向前或向后),大小为(1+$\frac{2m}{M}$)v0(水的阻力不计).分析 水的阻力不计,小孩a、小孩b和小船系统动量守恒,根据动量守恒定律列式求解,也可以先对小孩a跳出过程运用动量守恒定律,再对小孩b跳出过程运用动量守恒定律求小船的速度.
解答 解:设小孩b跃出后小船的速度为v′,取小船原来的速度方向为正,根据动量守恒定律,有
(M+2m)v0=Mv′+mυ-mυ
解得 v′=(1+$\frac{2m}{M}$)v0,方向向前.
故答案为:向前,(1+$\frac{2m}{M}$)v0.
点评 本题的关键选择两个小孩都跳出的整个过程运用动量守恒定律列式求解,若对小孩a跳出过程和小孩b跳出过程分开列式求解也可,但没有第一种方法简洁.

练习册系列答案
相关题目
7.空间某一区域内同时存在匀强电场和匀强磁场,一个带电粒子以某一速度射入该区域,不计粒子的重力,则带电粒子在此区域的运动可能是( )
| A. | 匀速直线运动 | B. | 匀速圆周运动 | ||
| C. | 加速度不变,速度先减小再增大 | D. | 加速度不变,速度先增大再减小 |
4.如图1所示,abcd是位于竖直平面内的正方形闭合金属线框,在金属线框的正下方有一匀强磁场区域,MN和PQ是匀强磁场区域的水平边界,并与线框的bc边平行,磁场方向与线框平面垂直.现金属线框由距MN的某一高度从静止开始下落,图2是金属线框由开始下落到完全穿过匀强磁场区域过程的速度一时间图象,己知金属线框的质量为m,当地的重力加速度为g,图象中坐标轴上所标出的字母均为己知量.根据题中所给条件,以下说法正确的是( )
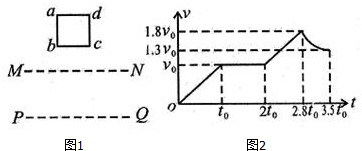

| A. | 可以求出金属框的边长 | |
| B. | 可以求出磁场的磁感应强度 | |
| C. | 可以求出金属线框在进入磁场过程中通过线框某一横截面的电荷量 | |
| D. | 可以求出金属线框在整个下落过程中所产生的热量 |
18.关于气体的内能,下列说法正确的是( )
| A. | 装有一定质量气体的密闭容器沿水平方向加速运动,气体的内能将不断增大 | |
| B. | 质量和温度都相同的理想气体,内能可能不同 | |
| C. | 标准情况下,1mol任何种类的理想气体其内能都相同 | |
| D. | 一定量的某种理想气体在等压膨胀过程中,内能一定增加 | |
| E. | 一定量的某种理想气体在绝热变化过程中,内能一定不变 |
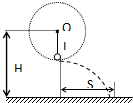 如图所示,用细线把小球悬挂在墙壁的钉子O上,小球绕悬点O在竖直平面内做圆周运动.小球质量为2kg,绳长L为0.8m,悬点距地面高度为1.6m.小球运动至最低点时,绳恰好被拉断,小球着地时速度与水平成45°,当地重力加速度为10m/s2.求:
如图所示,用细线把小球悬挂在墙壁的钉子O上,小球绕悬点O在竖直平面内做圆周运动.小球质量为2kg,绳长L为0.8m,悬点距地面高度为1.6m.小球运动至最低点时,绳恰好被拉断,小球着地时速度与水平成45°,当地重力加速度为10m/s2.求: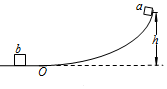 如图所示,光滑的轨道固定在竖直平面内,其O点左边为水平轨道,O点右边的曲线轨道高度h=0.80m,左右两段轨道在O点平滑连接.质量m=0.10kg的小滑块a由静止开始从曲线轨道的顶端沿轨道下滑,到达水平段后与处于静止状态的质量M=0.20kg的小滑块b发生碰撞,碰撞后小滑块a恰好停止运动.取重力加速度g=10m/s2,求:
如图所示,光滑的轨道固定在竖直平面内,其O点左边为水平轨道,O点右边的曲线轨道高度h=0.80m,左右两段轨道在O点平滑连接.质量m=0.10kg的小滑块a由静止开始从曲线轨道的顶端沿轨道下滑,到达水平段后与处于静止状态的质量M=0.20kg的小滑块b发生碰撞,碰撞后小滑块a恰好停止运动.取重力加速度g=10m/s2,求: