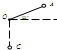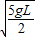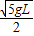题目内容
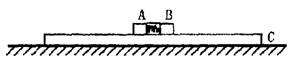
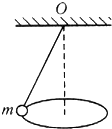长为L的细线，拴一质量为m的小球，一端固定于O点．让其在水平面内做匀速圆周运动（这种运动通常称为圆锥摆运动），如图所示．当摆线L与竖直方向的夹角是α时，求：（1）线的拉力F；
（2）小球运动的角速度．
分析：小球在重力和拉力合力作用下做圆周运动，靠两个力的合力提供向心力，根据牛顿第二定律求出角速度．
解答：解：对小球，受力分析如图：
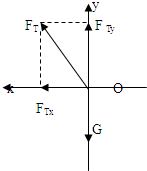
据牛顿第二定律：
FTy-G=0 ①
FTx=mω2r ②
又FTy=FT．cosα ③
FTx=FT．sinα ④
由①②③④，得：
FT=
，ω=
答：（1）线的拉力为
；
（2）小球运动的角速度为
．
据牛顿第二定律：
FTy-G=0 ①
FTx=mω2r ②
又FTy=FT．cosα ③
FTx=FT．sinα ④
由①②③④，得：
FT=
| mg |
| cosα |
|
答：（1）线的拉力为
| mg |
| cosα |
（2）小球运动的角速度为
|
点评：解决本题的关键搞清小球做圆周运动向心力的来源，运用牛顿第二定律进行求解．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，一根长为L的轻质细线，一端固定于O点，另一端拴有一质量为m的小球，可在竖直的平面内绕O点摆动，现拉紧细线使小球位于与O点在同一竖直面内的A位置，细线与水平方向成30°角，从静止释放该小球，当小球运动至悬点正下方C位置时的速度是（ ）
