题目内容
如图所示,长为L的木板C放在光滑水平面上,板上有两个小物块A和B,其间有一根用细线拴住的被压缩的轻质弹簧(弹簧与物块不相连),其弹性势能为E0,弹簧长度与L相比可忽略;且A、B、C三者的质量为mA=mc=m,mB=2m。A与C之间的动摩擦因数是B与C之间的动摩擦数的2倍,现将细线烧断,A、B被弹开向两边运动。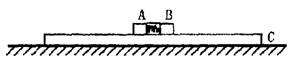
(1)A、B在C上运动时,C是否运动?若有,则方向如何,若没有,说明理由?
(2)若A、B运动停止时都正好停在C的两端,求A、B在C上滑行的距离LA=LB之比。
(3)若一开始A、B处于C的正中央,烧断细线后,哪个物体会先滑离C?滑离时其动能为多大?最终C的动能为多大?
解(1)A、B在C上运动时,C不会动 设:B与C间摩擦系数为
设:B与C间摩擦系数为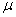 则A与C间的摩擦系数为2
则A与C间的摩擦系数为2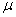
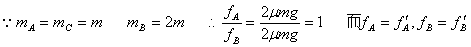 C受合力为零,故不动(2)
C受合力为零,故不动(2)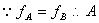 、B为系统在C上滑行时动量守恒,且系统的初动量为零。∴A、B一定同时停止运动。设A、B在弹簧恢复原长时的初动能分别为EKA ,EKB
、B为系统在C上滑行时动量守恒,且系统的初动量为零。∴A、B一定同时停止运动。设A、B在弹簧恢复原长时的初动能分别为EKA ,EKB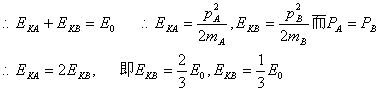 ∵弹簧长度与L相比可忽略,∴由动能定理:对A:
∵弹簧长度与L相比可忽略,∴由动能定理:对A: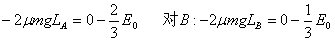
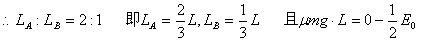 ①(3)置AB与C板中央,由题意易知:A先离开C板对A:
①(3)置AB与C板中央,由题意易知:A先离开C板对A: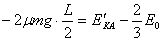 ② 将①代入解得
② 将①代入解得 又
又
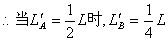 即当A滑离C时,B在C上滑动了
即当A滑离C时,B在C上滑动了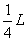 对B:
对B: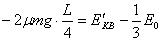 ③ 将①代入解得
③ 将①代入解得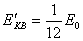 ④此后设B与C达到共同速度
④此后设B与C达到共同速度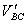 时,B还未离开C板
时,B还未离开C板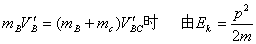
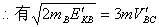 将④代入解得
将④代入解得 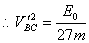 BC为系统的末动能即为
BC为系统的末动能即为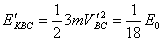 ⑤B与C上相对滑动的距离设为
⑤B与C上相对滑动的距离设为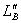
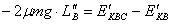 将①④⑤代入解得:
将①④⑤代入解得: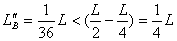 ∴最终BC共同运动
∴最终BC共同运动 
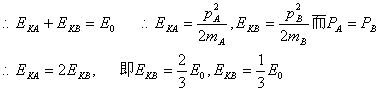 ∵弹簧长度与L相比可忽略,∴由动能定理:对A:
∵弹簧长度与L相比可忽略,∴由动能定理:对A:
练习册系列答案
相关题目
 如图所示,长L=34.5m的水平传送带以大小为υ=3m/s的速度沿逆时针方向运动,将一质量为M=2kg的小木盒B轻轻放在传送带右端,B与传送带之间的动摩擦因数μ=0.3,在木盒放上传送带的同时,有一个光滑的质量为m=1kg的小球A自传送带的左端以υ0=15m/s的速度在传送带上向右运动.球与木盒相遇时,木盒与传送带已相对静止,相遇后球立即进入盒中与盒保持相对静止.(取g=10m/s2)求:
如图所示,长L=34.5m的水平传送带以大小为υ=3m/s的速度沿逆时针方向运动,将一质量为M=2kg的小木盒B轻轻放在传送带右端,B与传送带之间的动摩擦因数μ=0.3,在木盒放上传送带的同时,有一个光滑的质量为m=1kg的小球A自传送带的左端以υ0=15m/s的速度在传送带上向右运动.球与木盒相遇时,木盒与传送带已相对静止,相遇后球立即进入盒中与盒保持相对静止.(取g=10m/s2)求: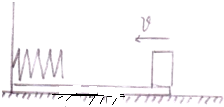 如图所示,质量为M=4kg长L=2.6m的木滑板静止放在光滑的水平面上,滑板的左端固定有一根劲度系数k=500N/m,原长L0=0.2m的轻弹簧,现有一质量m=1kg的小物块以V0=10m/s的速度从木滑板的右端滑上木板,物块接触弹簧后压缩弹簧,最后又恰好返回木板的右端,已知物块与木板间的动摩擦因数μ=0.8,求物块压缩弹簧的过程中受到弹簧的最大弹力.
如图所示,质量为M=4kg长L=2.6m的木滑板静止放在光滑的水平面上,滑板的左端固定有一根劲度系数k=500N/m,原长L0=0.2m的轻弹簧,现有一质量m=1kg的小物块以V0=10m/s的速度从木滑板的右端滑上木板,物块接触弹簧后压缩弹簧,最后又恰好返回木板的右端,已知物块与木板间的动摩擦因数μ=0.8,求物块压缩弹簧的过程中受到弹簧的最大弹力.

 )
)