题目内容
A、B两球(视为质点)质量分别为m1与m2,用一劲度系数为K的轻质弹簧相连,一长为l1的细线与B球相连,置于水平光滑桌面上,细线的另一端拴在竖直轴OO′上,如图所示.当m1与m2均以角速度ω绕竖直轴OO'做匀速圆周运动时,弹簧长度为l2.求:(1)弹簧原长l多大?
(2)绳子张力多大?

【答案】分析:B球绕OO′做匀速圆周运动,靠弹簧的弹力提供向心力,求出弹簧的弹力,根据胡克定律即可得出弹簧的伸长量.A球在水平方向上受绳子的拉力和弹簧的弹力,两个力合力提供A球做圆周运动的向心力,从而求出绳子的拉力.
解答:解:(1)对A进行受力分析,由牛顿第二定律得:
F=kx=m1(l1+l2)ω2
解得:
x=
l=l2-x=l2-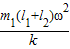
(2)对B进行受力分析,由牛顿第二定律得:
T-F=m2llω2
解得:T=F+m2l1ω2=m1(l1+l2)ω2+m2l1ω2
答:(1)弹簧原长l为l2-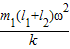 ;
;
(2)绳子张力为:m1(l1+l2)ω2+m2l1ω2
点评:解决本题的关键知道匀速圆周运动的向心力靠合力提供,A、B两球的角速度相同,难度适中.
解答:解:(1)对A进行受力分析,由牛顿第二定律得:
F=kx=m1(l1+l2)ω2
解得:
x=

l=l2-x=l2-
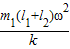
(2)对B进行受力分析,由牛顿第二定律得:
T-F=m2llω2
解得:T=F+m2l1ω2=m1(l1+l2)ω2+m2l1ω2
答:(1)弹簧原长l为l2-
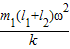 ;
;(2)绳子张力为:m1(l1+l2)ω2+m2l1ω2
点评:解决本题的关键知道匀速圆周运动的向心力靠合力提供,A、B两球的角速度相同,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
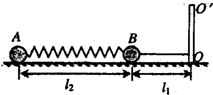 A、B两球(视为质点)质量分别为m1与m2,用一劲度系数为K的轻质弹簧相连,一长为l1的细线与B球相连,置于水平光滑桌面上,细线的另一端拴在竖直轴OO′上,如图所示.当m1与m2均以角速度ω绕竖直轴OO'做匀速圆周运动时,弹簧长度为l2.求:
A、B两球(视为质点)质量分别为m1与m2,用一劲度系数为K的轻质弹簧相连,一长为l1的细线与B球相连,置于水平光滑桌面上,细线的另一端拴在竖直轴OO′上,如图所示.当m1与m2均以角速度ω绕竖直轴OO'做匀速圆周运动时,弹簧长度为l2.求: 如图所示,MN为3m宽的小沟,M点左侧1m处有一5m高的平台与半径为1.25m的
如图所示,MN为3m宽的小沟,M点左侧1m处有一5m高的平台与半径为1.25m的 圆弧底部相切,平台表面与圆轨道都光滑,一质量为3kg的B球静止在平台上.现让一小球A从圆弧左侧与圆心等高处静止释放,A球下滑至平台并与B球发生碰撞.A、B两球可视为质点,g=10m/s2.求:
圆弧底部相切,平台表面与圆轨道都光滑,一质量为3kg的B球静止在平台上.现让一小球A从圆弧左侧与圆心等高处静止释放,A球下滑至平台并与B球发生碰撞.A、B两球可视为质点,g=10m/s2.求:
