题目内容
 如图所示,一根长为L的轻质细线,一端固定于O点,另一端拴有一质量为m的小球,可在竖直的平面内绕O点摆动,现拉紧细线使小球位于与O点在同一竖直面内的A位置,细线与水平方向成30°角,从静止释放该小球,当小球运动至悬点正下方C位置时的速度是( )
如图所示,一根长为L的轻质细线,一端固定于O点,另一端拴有一质量为m的小球,可在竖直的平面内绕O点摆动,现拉紧细线使小球位于与O点在同一竖直面内的A位置,细线与水平方向成30°角,从静止释放该小球,当小球运动至悬点正下方C位置时的速度是( )分析:对小球进行受力分析,小球开始做自由落体运动,下落到A与水平面的对称点B时细线将张紧,悬绳从伸直到对小球有拉力为止的短暂过程中,小球的速度是竖直向下的,那么,绳子的拉力与小球速度的夹角不等于90°,而是120°,由于惯性小球要继续竖直向下,那么伸直了的绳子就对小球施加拉力而做功,这个功可是负功.
小球由B运动至C,绳子的拉力与运动方向垂直不做功,只有重力做功,根据机械能守恒进行求解.
小球由B运动至C,绳子的拉力与运动方向垂直不做功,只有重力做功,根据机械能守恒进行求解.
解答:解:对小球进行受力分析及运动过程分析如下图所示.
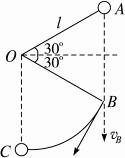
从静止释放小球,细线松弛,小球只受重力做自由落体运动,下落到A与水平面的对称点B时细线将张紧,
根据自由落体运动的规律
则vB=
方向竖直向下.
在B位置细线突然张紧,对小球施以冲量,使小球竖直向下的速度变为沿圆弧切线方向上的速度,vB′=vBcos30°,
小球的动能在瞬间减少,根据功能关系只能是绳子突然张紧“爆发”做功使机械能部分变为其他形式的能量(声能、内能等).
小球由B运动至C,绳子的拉力与运动方向垂直不做功,只有重力做功,机械能守恒.
此过程中,重力势能减少量△Ep=mgl(1-cos60°)
动能的增加量△Ek=
mvC2-
mv′B2?
有mgl(1-cos60°)=
mvC2-
mv′B2?
代入vB′=vBcos30°=
cos30°
得vC=
.?
故选A.

从静止释放小球,细线松弛,小球只受重力做自由落体运动,下落到A与水平面的对称点B时细线将张紧,
根据自由落体运动的规律
则vB=
| 2gL |
在B位置细线突然张紧,对小球施以冲量,使小球竖直向下的速度变为沿圆弧切线方向上的速度,vB′=vBcos30°,
小球的动能在瞬间减少,根据功能关系只能是绳子突然张紧“爆发”做功使机械能部分变为其他形式的能量(声能、内能等).
小球由B运动至C,绳子的拉力与运动方向垂直不做功,只有重力做功,机械能守恒.
此过程中,重力势能减少量△Ep=mgl(1-cos60°)
动能的增加量△Ek=
| 1 |
| 2 |
| 1 |
| 2 |
有mgl(1-cos60°)=
| 1 |
| 2 |
| 1 |
| 2 |
代入vB′=vBcos30°=
| 2gL |
得vC=
|
故选A.
点评:对本题要进行层层深入的分析方式,不要忽视了悬绳从伸直到对小球有拉力为止的短暂过程中,机械能的损失,
不能直接对小球从初位置到末位置列机械能守恒的方程求最低点速度.
不能直接对小球从初位置到末位置列机械能守恒的方程求最低点速度.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图所示,一根长为L,质量不计的硬杆,在中点及右端各固定一个质量为m的小球,杆可带动小球在竖直平面内绕O点转动.若开始时杆处于水平位置,由静止开始释放,当杆下落到竖直位置时,下列说法中正确的是( )
如图所示,一根长为L,质量不计的硬杆,在中点及右端各固定一个质量为m的小球,杆可带动小球在竖直平面内绕O点转动.若开始时杆处于水平位置,由静止开始释放,当杆下落到竖直位置时,下列说法中正确的是( )A、B球的速率为
| ||||
B、B球的机械能减少了
| ||||
C、A球的机械能减少了
| ||||
| D、每个小球的机械能都不变 |
 如图所示,一根长为L的细杆的一端固定一质量为m的小球,整个系统绕杆的另一端在竖直面内做圆周运动,且小球恰能过最高点.已知重力加速度为g,细杆的质量不计.下列说法正确的是( )
如图所示,一根长为L的细杆的一端固定一质量为m的小球,整个系统绕杆的另一端在竖直面内做圆周运动,且小球恰能过最高点.已知重力加速度为g,细杆的质量不计.下列说法正确的是( )A、小球过最低点时的速度大小为
| ||
B、小球过最高点时的速度大小为
| ||
| C、小球过最低点时受到杆的拉力大小为5mg | ||
| D、小球过最高点时受到杆的支持力为零 |
 如图所示,一根长为L、质量为100kg的木头,其重心O在离粗端
如图所示,一根长为L、质量为100kg的木头,其重心O在离粗端 如图所示,一根长为l的轻杆的一端与一个质量为m为小球相连,并可绕过另一端O点的水平轴在竖直面内自由转动,图中的a、b分别表示小球运动轨迹的最低点和最高点,已知杆能提供的最大支持力为
如图所示,一根长为l的轻杆的一端与一个质量为m为小球相连,并可绕过另一端O点的水平轴在竖直面内自由转动,图中的a、b分别表示小球运动轨迹的最低点和最高点,已知杆能提供的最大支持力为