Question

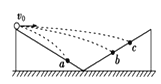
【题目】同学们参照伽利略时期演示平抛运动的方法制作了如图所示的实验装置．图中水平放置的底板上竖直地固定有M板和N板．M板上部有一半径为R的圆弧形的粗糙轨道，P为最高点，Q为最低点，Q点处的切线水平，距底板高为H，N板上固定有三个圆环．将质量为m的小球从P处静止释放，小球运动至Q飞出后无阻碍地通过各圆环中心，落到底板上距Q水平距离为L处．不考虑空气阻力，重力加速度为g．求：

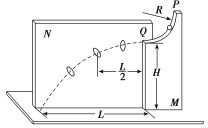
（1）距Q水平距离为的圆环中心到底板的高度；

（2）小球运动到Q点时速度的大小以及对轨道压力的大小和方向；

（3）摩擦力对小球做的功．

Answer 1

【答案】（1）到底板的高度：H

（2）速度的大小：L 压力的大小：mg

方向：竖直向下

（3）摩擦力对小球做的功：mg

【解析】

试题分析：（1）设小球在Q点的速度为v0，由平抛运动规律有H＝gt，L＝v0t1，得v0＝L ．从Q点到距Q点水平距离为的圆环中心的竖直高度为h，则＝v0t2，得h＝gt＝H．

该位置距底板的高度：Δh＝H－h＝H．

（2）设小球在Q点受的支持力为F，由牛顿第二定律F－mg＝m，得F＝mg，由牛顿第三定律可知，小球对轨道的压力F′＝F，方向竖直向下．

（3）设摩擦力对小球做功为W，则由动能定理得

mgR＋W＝mv

得W＝mg．