题目内容
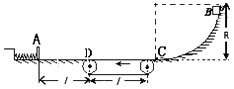
【题目】如图，轻质弹簧一端固定在水平面上O点的转轴上，另一端与一质量为m、套在粗糙固定直杆A处的小球（可视为质点）相连，直杆的倾角为37°，OA=OC，B为AC的中点，OB等于弹簧原长，小球从A处由静止开始下滑，初始加速度大小为aA ， 第一次经过B处的速度为v，运动到C处速度为零，后又以大小为aC的初始加速度由静止开始向上滑行，设最大静摩擦力等于滑动摩擦力，下列说法正确的是（ ）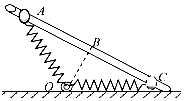
A.小球能返回到出发点A处
B.弹簧具有的最大弹性势能为 
C.撤去弹簧，小球不可能在直杆上处于静止
D.aA﹣aC=2gsin37°
【答案】B,C,D
【解析】解：AB、设小球从A运动到B的过程克服摩擦力做功为Wf，AB间的竖直高度为h，小球的质量为m，弹簧具有的最大弹性势能为Ep．
根据能量守恒定律得：
对于小球A到B的过程有：mgh+Ep= 
mv2+Wf，
A到C的过程有：2mgh+Ep=2Wf+Ep，解得：Wf=mgh，Ep= mv2．
小球从C点向上运动时，假设能返回到A点，则由能量守恒定律得：
Ep=2Wf+2mgh+Ep，该式违反了能量守恒定律，可知小球不能返回到出发点A处．A不符合题意，B符合题意．
C、设从A运动到C摩擦力的平均值为 
，AB=s，由Wf=mgh得： s=mgssin37°
在B点，摩擦力 f=μmgcos37°，由于弹簧对小球有拉力（除B点外），小球对杆的压力大于μmgcos37°，所以 ＞μmgcos37°
可得 mgsin37°＞μmgcos37°，因此撤去弹簧，小球不能在直杆上处于静止．C符合题意．
D、根据牛顿第二定律得：
在A点有：Fcos37°+mgsin37°﹣f=maA；
在C点有：Fcos37°﹣f﹣mgsin37°=maC；
两式相减得：aA﹣aC=2gsin37°．D符合题意．
故答案为：BCD
小球运动的过程，满足能量守恒，根据能量守恒定律结合摩擦力做功的特点以及牛顿第二运动定律，综合列式求解。
