题目内容
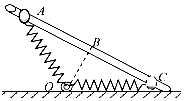
【题目】如图所示,装置左边是水平台面,一轻质弹簧左端固定,右端连接轻质挡板A,此时弹簧处于原长且在A右侧台面粗糙,长度l=1.0m,另一物块B与台面动摩擦因数μ1=0.1,中间水平传送带与平台和右端光滑曲面平滑对接,传送带始终以V0=2m/s速率逆时针转动,传送带长度l=1.0m,B与传送带动摩擦因数μ2=0.2,现将质量为1kg的物块B从半径R=2.1m的 ![]() 圆弧上静止释放(g=10m/s2)
圆弧上静止释放(g=10m/s2)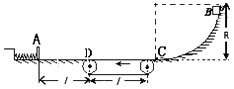
(1)求物块B与A第一次碰撞前的速度大小;
(2)试通过计算证明物块B与A第一次碰撞后能否运动到右边的弧面上?若能回到,则其回到C点时受弧面的支持力为多大?
【答案】
(1)解:设物块B沿光滑曲面下滑到C点的速度为vC,与A物体碰撞前的速度大小为v.物块B下滑过程,由动能定理知:
mBgh= ![]() mBvC2
mBvC2
代入数据解得:vC= ![]() m/s
m/s
滑上转送带速度减为v0,发生的位移为x.由动能定理得:
![]() mBvC2﹣
mBvC2﹣ ![]() mBv02=﹣2μ2mBgx
mBv02=﹣2μ2mBgx
代入数据解得:x=9.5m>1m
物块B从开始下滑到与A碰撞前的过程,由动能定理得:
mBgh﹣μ1mBgl﹣μ2mBgl= ![]() mBv2
mBv2
代入数据解得:v=6 m/s
答:物块B与A第一次碰撞前的速度大小为6m/s.
(2)设物块B在传送带上向右运动的最大位移为l′,则由动能定理得:
0﹣ ![]() mBv2=﹣μ1mBgl﹣μ2mBgl′
mBv2=﹣μ1mBgl﹣μ2mBgl′
代入数据解得:l′=8.5m>1m
所以物块B能通过传送带运动到右边的曲面上.
设物体B到达C点速度为v1,由动能定理可知: ![]() mBv2﹣μ1mBgl﹣μ2mBgl=
mBv2﹣μ1mBgl﹣μ2mBgl= ![]() mBv12
mBv12
代入数据解得:v1= ![]() m/s
m/s
在C点:FN﹣mg=m ![]()
代入数据解得:FN= ![]() N
N
答:物块B能通过传送带运动到右边的曲面上.其回到C点时受弧面的支持力为 ![]() N.
N.
【解析】(1)物块B沿光滑曲面下滑的过程,只有重力做功,根据动能定理列出求出滑到C点的速度.和速度减至时v0时发生的位移,可判断出物块能否滑上左侧平台,再根据动能定理求物块B与A第一次碰撞前的速度大小.
(2)对物块返回过程,由动能定理求出速度减至零时发生的位移,即可判断能否运动到右边的弧面上.根据合外力等于向心力求出支持力大小.

 阅读快车系列答案
阅读快车系列答案