Question

【题目】如图所示，在一个倾角θ=30°的斜面上建立x轴，O为坐标原点，在x轴正向空间有一个匀强电场，场强大小E=4.5×106N/C，方向与x轴正方向相同，在O处放一个电荷量q=5.0×10﹣6C，质量m=lkg带负电的绝缘物块．物块与斜面间的动摩擦因数μ= ，沿x轴正方向给物块一个初速度V0=5m/s，如图所示（g取10m/s2）．求：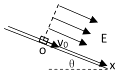

（1）物块沿斜面向下运动的最大距离为多少？
（2）到物块最终停止时系统产生的焦耳热共为多少？

Answer 1

【答案】
（1）解：设物块向下运动的最大距离为 x m，由动能定理得：

mgsinθxm﹣μmgcosθxm﹣qExm=0﹣ ，

代入数据可求得：xm=0.5m．

答：物块沿斜面向下运动的最大距离为0.5m；

（2）因qE＞mgsinθ+μmgcosθ，物块不可能停止在 x轴正向，设最终停在 x轴负向且离O点为 x 处，

整个过程电场力做功为零，由动能定理得：

﹣mgxsinθ﹣μmgcosθ（2xm+x）=0 ，

代入数据可得：x=0.4m．

产生的焦耳热：Q=μmgcosθ（2xm+x），

代入数据解得Q=10.5J．

答：到物块最终停止时系统产生的焦耳热共为10.5J．

【解析】（1）利用动能定理求出五块沿斜面向下运动最大距离为多少。
（2）物块，在运动过程中，只有电场力和摩擦力做功，利用动能定理求出移动的距离。摩擦力对物体所做的功就是摩擦所产生的热量。