题目内容
14. 为测定木块与斜面间的动摩擦因数,某同学让木块从斜面上端自静止起做匀加速下滑运动(如图所示),他使用的实验器材仅限于:①倾角固定的斜面(倾角未知);②木块;③秒表;④米尺;(重力加速度为g).
为测定木块与斜面间的动摩擦因数,某同学让木块从斜面上端自静止起做匀加速下滑运动(如图所示),他使用的实验器材仅限于:①倾角固定的斜面(倾角未知);②木块;③秒表;④米尺;(重力加速度为g).(1)实验中应记录的数据是L、h、d、t
(2)用上述测量数据表示计算动摩擦因数的公式是μ=$\frac{h}{d}$-$\frac{2{L}^{2}}{gd{t}^{2}}$
(3)为了减小测量的误差,可采用的办法是多次测量取平均值、斜面的倾角适当小些、斜面长度适当长些.
分析 木块沿斜面下滑,用刻度尺测出斜面的长度,即木块的位移,用秒表测出木块的运动时间,由匀变速运动的位移公式可以求出木块的加速度;再用刻度尺测出斜面的高度,由数学知识求出斜面的倾角;最后对木块进行受力分析,由牛顿第二定律列方程,然后求出动摩擦因数.
解答 解:实验中需要测出:斜面的长度L,斜面的高度h,斜面的底面边长d,木块下滑的时间t;
木块做初速度为零的匀加速运动,则L=$\frac{1}{2}$at2,木块的加速度a=$\frac{2L}{{t}^{2}}$;
对木块,由牛顿第二定律得:mgsinθ-μmgcosθ=ma,
设斜面倾角为θ,sinθ=$\frac{h}{L}$,cosθ=$\frac{d}{L}$,
解得:μ=$\frac{h}{d}$-$\frac{2{L}^{2}}{gd{t}^{2}}$;
多次测量求平均值可以减小实验误差,还有斜面的倾角适当小些、斜面长度适当长些这两种方法.
故答案为:(1)L、h、d、t;(2)$\frac{h}{d}$-$\frac{2{L}^{2}}{gd{t}^{2}}$;多次测量求平均值.
(3)多次测量取平均值、斜面的倾角适当小些、斜面长度适当长些
点评 物体沿斜面下滑是一个重要的物理模型,这类问题变化多样,包含丰富的物理知识,一定要对该过程中摩擦力、弹力、重力沿斜面的分力、加速度等物理量的变化分析透彻.

练习册系列答案
相关题目
4.从同一高度做自由落体运动的甲、乙两个小铁球,甲的质量是乙的两倍,则( )
| A. | 甲比乙先落地,落地时甲的速度是乙的两倍 | |
| B. | 甲比乙先落地,落地时甲、乙的速度相同 | |
| C. | 甲、乙同时落地,落地时甲的速度是乙的两倍 | |
| D. | 甲、乙同时落地,落地时甲、乙的速度相同 |
5. 如图所示,一竖直方向的电场线上有A、B两点,若将带正电物体在A点从静止释放,沿竖直方向下落,经过B点时速度为零,则这一过程中( )
如图所示,一竖直方向的电场线上有A、B两点,若将带正电物体在A点从静止释放,沿竖直方向下落,经过B点时速度为零,则这一过程中( )
 如图所示,一竖直方向的电场线上有A、B两点,若将带正电物体在A点从静止释放,沿竖直方向下落,经过B点时速度为零,则这一过程中( )
如图所示,一竖直方向的电场线上有A、B两点,若将带正电物体在A点从静止释放,沿竖直方向下落,经过B点时速度为零,则这一过程中( )| A. | 物体的电场力做正功 | |
| B. | 电场方向由A指B | |
| C. | 物体的运动不可能是匀加速运动 | |
| D. | 物体重力做功大于克服电场力所做的功 |
9. 如图所示,一条质量分布均匀的长度为L的铁链置于光滑水平桌面上.用手按着一端,使另一端长L0的一段下垂.放开手后使铁链从静止开始下滑,当铁链完全通过桌边的瞬间时,铁链具有的速率为( )
如图所示,一条质量分布均匀的长度为L的铁链置于光滑水平桌面上.用手按着一端,使另一端长L0的一段下垂.放开手后使铁链从静止开始下滑,当铁链完全通过桌边的瞬间时,铁链具有的速率为( )
 如图所示,一条质量分布均匀的长度为L的铁链置于光滑水平桌面上.用手按着一端,使另一端长L0的一段下垂.放开手后使铁链从静止开始下滑,当铁链完全通过桌边的瞬间时,铁链具有的速率为( )
如图所示,一条质量分布均匀的长度为L的铁链置于光滑水平桌面上.用手按着一端,使另一端长L0的一段下垂.放开手后使铁链从静止开始下滑,当铁链完全通过桌边的瞬间时,铁链具有的速率为( )| A. | $\sqrt{\frac{g({L}^{2}+{L}_{0}^{2})}{{L}_{0}}}$ | B. | $\sqrt{g(L-{L}_{0})}$ | C. | $\sqrt{g(L+{L}_{0})}$ | D. | $\sqrt{\frac{g({L}^{2}-{L}_{0}^{2})}{L}}$ |
6.物理学家在微观领域发现了“电子偶素”这一现象.所谓“电子偶素”就是由一个负电子和一个正电子绕它们连线的中点,做匀速圆周运动形成相对稳定的系统.类比玻尔的原子量子化模型可知:两电子做圆周运动的可能轨道半径的取值是不连续的,所以“电子偶素”系统对应的能量状态(能级)也是不连续的.若规定两电子相距无限远时该系统的引力势能为零,则该系统的最低能量值为E(E<0),称为“电子偶素”的基态,基态对应的电子运动的轨道半径为r.已知正、负电子的质量均为m,电荷量大小均为e,静电力常量为k,普朗克常量为h.则下列说法中正确的是( )
| A. | “电子偶素”系统处于基态时,一个电子运动的动能为$\frac{{k{e^2}}}{8r}$ | |
| B. | “电子偶素”系统吸收特定频率的光子发生能级跃迁后,电子做圆周运动的动能增大 | |
| C. | 处于激发态的“电子偶素”系统向外辐射光子的最大波长为-$\frac{hc}{E}$ | |
| D. | 处于激发态的“电子偶素”系统向外辐射光子的最小频率为-$\frac{E}{h}$ |
4.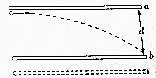 水平平行放置的金属板a、b间加上恒定电压U,两板间距离为d.一带电粒子紧贴a板水平射入电场,刚好紧贴b板射出,如图所示.在其他条件不变的情况下,仅将b板向下平移一段距离x,或仅将电压减小△U,带电粒子均刚好从两板右侧中央射出.不考虑重力的影响,则( )
水平平行放置的金属板a、b间加上恒定电压U,两板间距离为d.一带电粒子紧贴a板水平射入电场,刚好紧贴b板射出,如图所示.在其他条件不变的情况下,仅将b板向下平移一段距离x,或仅将电压减小△U,带电粒子均刚好从两板右侧中央射出.不考虑重力的影响,则( )
 水平平行放置的金属板a、b间加上恒定电压U,两板间距离为d.一带电粒子紧贴a板水平射入电场,刚好紧贴b板射出,如图所示.在其他条件不变的情况下,仅将b板向下平移一段距离x,或仅将电压减小△U,带电粒子均刚好从两板右侧中央射出.不考虑重力的影响,则( )
水平平行放置的金属板a、b间加上恒定电压U,两板间距离为d.一带电粒子紧贴a板水平射入电场,刚好紧贴b板射出,如图所示.在其他条件不变的情况下,仅将b板向下平移一段距离x,或仅将电压减小△U,带电粒子均刚好从两板右侧中央射出.不考虑重力的影响,则( )| A. | x=d | B. | x=($\sqrt{2}$-1)d | C. | △U=$\frac{1}{2}$U | D. | △U=($\sqrt{2}$-1)U |

 表演“水流星”节目,如图所示,拴杯子的绳子长为L,要使节目获得成功,绳子承受的拉力足够大,则杯子通过最高点时速度的最小值为$\sqrt{gL}$.
表演“水流星”节目,如图所示,拴杯子的绳子长为L,要使节目获得成功,绳子承受的拉力足够大,则杯子通过最高点时速度的最小值为$\sqrt{gL}$.