题目内容
20.小球A从高为H=40m的塔顶自由下落,同时小球B自塔底以速度v0=30m/s竖直上抛,若A、B两球在同一直线上运动,关于两球相遇的位置,下列说法正确的是( )| A. | 两球在B球上升过程中相遇 | B. | 两球在B球下降过程中相遇 | ||
| C. | 两球在B球运动的最高点相遇 | D. | 两球在空中没有相遇 |
分析 分别写出两个物体的运动方程,当它们相遇时,它们位移的和等于H.联立方程即可求出.
解答 解:A球做自由落体运动,位移的方向向下,大小为:${h}_{1}=\frac{1}{2}g{t}^{2}$
B物体位移的方向向上,大小为:${h}_{2}={v}_{0}t-\frac{1}{2}g{t}^{2}$
当它们相遇时,h1+h2=H
代入数据,联立得:t=$\frac{4}{3}$s
此时B的速度:${v}_{B}={v}_{0}-gt=30-10×\frac{4}{3}=16.7$m/s,与B的初速度方向相同,说明B仍然向上运动.
所以选项A正确,BCD错误.
孤星:A
点评 解决本题的关键知道两物体在空中相碰,两物体的位移之和等于H,结合物体运动时间的范围,求出初始度的范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 一根轻质细线将2个薄铁垫片A、B连接起来,一同学用手固定B,此时A、B间距为3L,A距地面为L,如图所示.由静止释放A、B,不计空气阻力,且A、B落地后均不再弹起.从开始释放到A落地历时t1,A落地前的瞬时速率为v1,从A落地到B落在A上历时t2,B落在A上前的瞬时速率为v2,则( )
一根轻质细线将2个薄铁垫片A、B连接起来,一同学用手固定B,此时A、B间距为3L,A距地面为L,如图所示.由静止释放A、B,不计空气阻力,且A、B落地后均不再弹起.从开始释放到A落地历时t1,A落地前的瞬时速率为v1,从A落地到B落在A上历时t2,B落在A上前的瞬时速率为v2,则( )
 一根轻质细线将2个薄铁垫片A、B连接起来,一同学用手固定B,此时A、B间距为3L,A距地面为L,如图所示.由静止释放A、B,不计空气阻力,且A、B落地后均不再弹起.从开始释放到A落地历时t1,A落地前的瞬时速率为v1,从A落地到B落在A上历时t2,B落在A上前的瞬时速率为v2,则( )
一根轻质细线将2个薄铁垫片A、B连接起来,一同学用手固定B,此时A、B间距为3L,A距地面为L,如图所示.由静止释放A、B,不计空气阻力,且A、B落地后均不再弹起.从开始释放到A落地历时t1,A落地前的瞬时速率为v1,从A落地到B落在A上历时t2,B落在A上前的瞬时速率为v2,则( )| A. | t1>t2 | B. | t1<t2 | C. | v1:v2=1:2 | D. | v1:v2=1:3 |
1.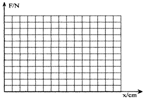 以下是一位同学做“探究形变与弹力的关系”的实验.
以下是一位同学做“探究形变与弹力的关系”的实验.
(1)下列的实验步骤是这位同学准备完成的,请你帮这位同学按操作的先后顺序,用字母排列出来是:CBDAEFG.
A、以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连结起来.
B、记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C、将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D、依次在弹簧下端挂上1个、2个、3个、4个…钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E、以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式.
F、解释函数表达式中常数的物理意义.
(2)下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
①算出每一次弹簧伸长量,并将结果填在上表的空格内
②在图的坐标上作出F-x图线.
③写出曲线的函数表达式.(x用cm作单位):F=0.43x;
④函数表达式中常数的物理意义:弹簧的劲度系数.
 以下是一位同学做“探究形变与弹力的关系”的实验.
以下是一位同学做“探究形变与弹力的关系”的实验.(1)下列的实验步骤是这位同学准备完成的,请你帮这位同学按操作的先后顺序,用字母排列出来是:CBDAEFG.
A、以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连结起来.
B、记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C、将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D、依次在弹簧下端挂上1个、2个、3个、4个…钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E、以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式.
F、解释函数表达式中常数的物理意义.
(2)下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
| 弹力(F/N) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| 弹簧原来长度(L0/cm) | 15 | 15 | 15 | 15 | 15 |
| 弹簧后来长度(L/cm) | 16.2 | 17.3 | 18.5 | 19.6 | 20.8 |
| 弹簧伸长量(x/cm) | 1.2 | 2.3 | 3.5 | 4.6 | 5.8 |
②在图的坐标上作出F-x图线.
③写出曲线的函数表达式.(x用cm作单位):F=0.43x;
④函数表达式中常数的物理意义:弹簧的劲度系数.
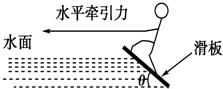 滑板运动是一项非常刺激的水上运动,研究表明,在进行滑板运动时,水对滑板的作用力FN垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时(如上图所示),滑板做匀速直线运动,相应的k=45kg/m,人和滑板的总质量为108kg,试求(重力加速度g取10m/s2,sin 37°=$\frac{3}{5}$,忽略空气阻力):
滑板运动是一项非常刺激的水上运动,研究表明,在进行滑板运动时,水对滑板的作用力FN垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时(如上图所示),滑板做匀速直线运动,相应的k=45kg/m,人和滑板的总质量为108kg,试求(重力加速度g取10m/s2,sin 37°=$\frac{3}{5}$,忽略空气阻力):
 如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度vA=4m/s.g取10m/s2,求:
如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度vA=4m/s.g取10m/s2,求: 某新型磁敏电阻的阻值RB与磁感应强度大小B的关系如图甲所示,其关系式为RB=140+1000B(Ω);用该磁敏电阻制作一个测量磁感应强度大小的磁感应强度测量仪,其制作步骤如下:
某新型磁敏电阻的阻值RB与磁感应强度大小B的关系如图甲所示,其关系式为RB=140+1000B(Ω);用该磁敏电阻制作一个测量磁感应强度大小的磁感应强度测量仪,其制作步骤如下: