题目内容
1.如图所示,在与水平方向成θ角的传送带上有质量均为m的三个木块1、2、3,中间均用原长为l、劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细线拉住,传送带按图示方向匀速运动,三个木块处于平衡状态.此时细线的拉力FT是多大?木块1、3之间的距离L13是多大?
分析 对木块1、2、3整体研究,由平衡条件求细线的拉力FT.再对木块3、木块2和3整体分别研究,由平衡条件和胡克定律结合求出2、3间弹簧伸长的长度和1、2间弹簧伸长的长度,即可得到1、3间的距离L13.
解答 解:(1)对木块1、2、3整体,由平衡条件可得:FT=3mgsinθ+3μmgcosθ
(2)对木块3有:mgsinθ+μmgcosθ=kx23
对木块2、3整体有:2mgsinθ+2μmgcosθ=kx12
则木块1、3间距:L13=2l+x12+x23=2l+$\frac{3(mgsinθ+μmgcosθ)}{k}$
答:此时细线的拉力FT是3mgsinθ+3μmgcosθ,木块1、3之间的距离L13是2l+$\frac{3(mgsinθ+μmgcosθ)}{k}$.
点评 本题关键是灵活地选择研究对象,然后根据共点力平衡条件列式求解出弹簧的伸长量.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 一滑雪运动员以一定的初速度从一平台上滑出,刚好落在一斜坡上的B点,且与斜坡没有撞击,则平台边缘A点和斜坡B点连线与竖直方向夹角α斜坡倾角θ的关系为( )
一滑雪运动员以一定的初速度从一平台上滑出,刚好落在一斜坡上的B点,且与斜坡没有撞击,则平台边缘A点和斜坡B点连线与竖直方向夹角α斜坡倾角θ的关系为( )
 一滑雪运动员以一定的初速度从一平台上滑出,刚好落在一斜坡上的B点,且与斜坡没有撞击,则平台边缘A点和斜坡B点连线与竖直方向夹角α斜坡倾角θ的关系为( )
一滑雪运动员以一定的初速度从一平台上滑出,刚好落在一斜坡上的B点,且与斜坡没有撞击,则平台边缘A点和斜坡B点连线与竖直方向夹角α斜坡倾角θ的关系为( )| A. | tanθ•$\frac{1}{tanα}$=2 | B. | tanθ•tanα=2 | C. | tanα.$\frac{1}{tanθ}$=2 | D. | tanθ•tanα=1 |
9.下列单位属于国际单位制中的基本单位的是( )
| A. | 安培 | B. | 库仑 | C. | 伏特 | D. | 牛顿 |
16. A、D两点分别是斜面的顶端、底端,B、C是斜面上的两个点,LAB=LBC=LCD,E点在D点正上方并与A点等高.从E点以不同的水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,从抛出到落在斜面上的过程(不计空气阻力)中,则球1和球2( )
A、D两点分别是斜面的顶端、底端,B、C是斜面上的两个点,LAB=LBC=LCD,E点在D点正上方并与A点等高.从E点以不同的水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,从抛出到落在斜面上的过程(不计空气阻力)中,则球1和球2( )
 A、D两点分别是斜面的顶端、底端,B、C是斜面上的两个点,LAB=LBC=LCD,E点在D点正上方并与A点等高.从E点以不同的水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,从抛出到落在斜面上的过程(不计空气阻力)中,则球1和球2( )
A、D两点分别是斜面的顶端、底端,B、C是斜面上的两个点,LAB=LBC=LCD,E点在D点正上方并与A点等高.从E点以不同的水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,从抛出到落在斜面上的过程(不计空气阻力)中,则球1和球2( )| A. | 运动时间之比为1:2 | B. | 抛出时初速度之比为x1 | ||
| C. | 动能增加量之比为1:2 | D. | 重力做功之比为1:3 |
6.(多选)某一物体从静止开始做直线运动,其加速度随时间变化的图线如图所示,则该物体( )


| A. | 第1 s末和第4 s末速度都是8 m/s | |
| B. | 第1 s内加速运动,第2、3 s内减速运动,第3 s末回到出发点 | |
| C. | 第3 s末速度为零,且运动方向不变 | |
| D. | 第3 s末速度为零,且此时开始改变运动方向 |
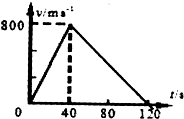 竖直升空的火箭,其速度图象如图所示,由图可知火箭加速上升的加速度为20m/s2,离地最大高度为48km.
竖直升空的火箭,其速度图象如图所示,由图可知火箭加速上升的加速度为20m/s2,离地最大高度为48km. 一质点向右做减速直线运动,经过A点的速度为15m/s,经过B点的速度为10m/s,经过C点的速度为0,又反向B运动,第二次经过B点的速度为30m/s,质点由A到B,B到C,C到B的时间分别为3s,5s,7s.
一质点向右做减速直线运动,经过A点的速度为15m/s,经过B点的速度为10m/s,经过C点的速度为0,又反向B运动,第二次经过B点的速度为30m/s,质点由A到B,B到C,C到B的时间分别为3s,5s,7s. 一个小球沿斜面向下运动,用每隔0.1s曝光一次的频闪照相机拍摄不同时刻小球位置的照片,如图所示,测得小球在A,B,C,D各点相当于O点的位移分别为OA=8.20cm,OB=17.49cm,OC=27.90cm,OD=39.39cm,则小车运动的加速度有多大?
一个小球沿斜面向下运动,用每隔0.1s曝光一次的频闪照相机拍摄不同时刻小球位置的照片,如图所示,测得小球在A,B,C,D各点相当于O点的位移分别为OA=8.20cm,OB=17.49cm,OC=27.90cm,OD=39.39cm,则小车运动的加速度有多大?