题目内容
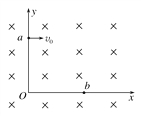
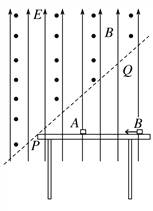
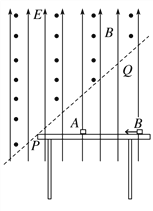
【题目】如图所示,水平桌面上方区域存在竖直向上的匀强电场,电场强度![]() 。过桌左边缘的虚线PQ上方存在垂直纸面向外的匀强磁场,磁感应强度
。过桌左边缘的虚线PQ上方存在垂直纸面向外的匀强磁场,磁感应强度![]() ,虚线PQ与水平桌面成45°角。现将一个质量
,虚线PQ与水平桌面成45°角。现将一个质量![]() 、带正电
、带正电![]() 的物块A静置在桌面上,质量
的物块A静置在桌面上,质量![]() 、不带电的绝缘物块B从与A相距
、不带电的绝缘物块B从与A相距![]() 处的桌面上以
处的桌面上以![]() 的初速度向左运动。物块A、B与桌面间的动摩擦因数均为
的初速度向左运动。物块A、B与桌面间的动摩擦因数均为![]() ,二者在桌面上发生弹性碰撞(碰撞时间极短),碰撞后B反弹速度为
,二者在桌面上发生弹性碰撞(碰撞时间极短),碰撞后B反弹速度为![]() ,A向左运动进入磁场。(结果保留两位有效数字)求:
,A向左运动进入磁场。(结果保留两位有效数字)求:
(1)碰撞后物块A的速度;
(2)A进入磁场到再次回到桌面所用时间;
(3)若一段时间后A、B在桌面上相遇,求碰撞前A与桌左边缘P的距离。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】(1)设B与A碰撞前瞬间的速度为![]() ,碰后A、B的速度分别为
,碰后A、B的速度分别为![]() 、
、![]()
对于B由动能定理可得: ![]()
A、B碰撞过程中,规定向左为正方向,对于A、B组成的系统由动量守恒定律可得: ![]()
联立可得: ![]() ,方向水平向左
,方向水平向左
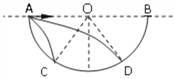
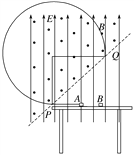
(2)对A受力分析可知![]() ,故碰撞后A向左匀速直线运动进入磁场,并在磁场中做匀速圆周运动,设在磁场中做圆周运动的周期为T,则:
,故碰撞后A向左匀速直线运动进入磁场,并在磁场中做匀速圆周运动,设在磁场中做圆周运动的周期为T,则: ![]()
由几何知识可得:A球在磁场中运动![]() 了个圆周,轨迹如图所示。
了个圆周,轨迹如图所示。
设A在磁场中运动的时间为![]() ,则:
,则: ![]()
A运动出磁场后竖直向下匀速运动再次回到桌面位置,设其运动时间为![]()
由题意可得:磁场中洛伦兹力提供向心力: ![]()
又![]() ,
, ![]()
联立得:t=2.7s
(3)碰撞后B反弹在桌面上做匀减速运动,设其加速度为a,停止运动所用时间为![]()
根据牛顿第二定律得: ![]()
根据速度时间公式得: ![]()
解得: ![]()
显然,碰撞后B运动时间小于A运动时间,由此可知A
B匀减速的位移: ![]()
根据题意,A距桌边P的距离: ![]()
所以可得:x=0.83m