题目内容
【题目】滑块a、b沿水平面上同一条直线发生碰撞；碰撞后两者粘在一起运动；经过一段时间后，从光滑路段进入粗糙路段。两者的位置x随时间t变化的图像如图所示。求：
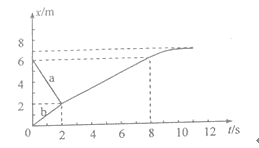
（ⅰ）滑块a、b的质量之比；
（ⅱ）整个运动过程中，两滑块克服摩擦力做的功与因碰撞而损失的机械能之比。
【答案】（1）1:8 （2）1:2
【解析】
试题分析：（1）设a、b的质量分别为m1、m2，a、b碰撞前地速度为v1、v2．
由题给的图象得
v1=-2m/s ①
v2=1m/s ②
a、b发生完全非弹性碰撞，碰撞后两滑块的共同速度为v．
由题给的图象得v=
m/s ③
由动量守恒定律得
m1v1+m2v2=（m1+m2）v ④
联立①②③④式得m1：m2=1：8
（ii）由能量守恒得，两滑块因碰撞损失的机械能为△E=
m1v12+m2v22（m1+m2）v2
由图象可知，两滑块最后停止运动，由动能定理得，两滑块克服摩擦力所做的功为
W=（m1+m2）v2
联立⑥⑦式，并代入数据得W：△E=1：2
练习册系列答案
相关题目
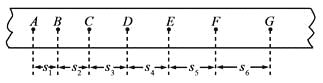
【题目】某同学利用图示装置研究小车的匀变速直线运动。
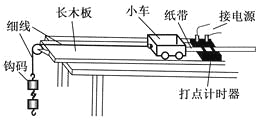
①实验中必要的措施是______。
A．细线必须与长木板平行 |
B．先接通电源再释放小车 |
C．小车的质量远大于钩码的质量 |
D．平衡小车与长木板间的摩擦力 |
②他实验时将打点计时器接到频率为50 HZ的交流电源上，得到一条纸带，打出的部分计数点如图所示（每相邻两个计数点间还有4个点，图中未画出）。s1="3.59" cm，s2="4.41" cm，s3="5.19" cm，s4="5.97" cm，s5="6.78" cm，s6="7.64" cm。则小车的加速度a=______m/s2（要求充分利用测量的数据），打点计时器在打B点时小车的速度vB=_______m/s。（结果均保留两位有效数字）
