题目内容
【题目】为了研究过山车的原理,某物理小组提出了下列的设想:取一个与水平方向夹角为![]() ,长为
,长为![]() 的倾斜轨道AB,通过微小圆弧与长为
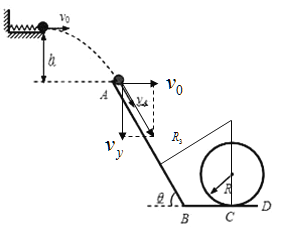
的倾斜轨道AB,通过微小圆弧与长为![]() 的水平轨道BC相连,然后在C处设计一个竖直完整的光滑圆轨道,出口为水平轨道D,如图所示。现将一个小球从距A点高为
的水平轨道BC相连,然后在C处设计一个竖直完整的光滑圆轨道,出口为水平轨道D,如图所示。现将一个小球从距A点高为![]() 的水平台面上以一定的初速度
的水平台面上以一定的初速度![]() 水平弹出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知小球与AB和BC间的动摩擦因数均为
水平弹出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知小球与AB和BC间的动摩擦因数均为![]() 。取
。取![]() 。
。
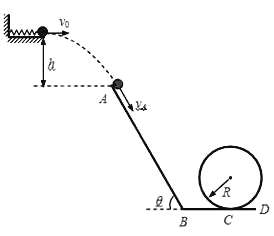
求:(1)小球初速度![]() 的大小;
的大小;
(2)小球滑过C点时的速率![]() ;
;
(3)要使小球不离开轨道,则竖直圆弧轨道的半径R应该满足什么条件。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 。
。
【解析】试题分析:(1)小球离开弹簧后做平抛运动到达A点,竖直方向:由![]() 可知
可知![]()
在A点的速度![]() 恰好沿AB方向,由几何关系可知:
恰好沿AB方向,由几何关系可知:![]()
水平方向分速度即小球的初速度![]()
(2)从A经B到C点的过程,由动能定理得:![]()
小球滑过C点时的速率![]()
(3)①若小球能通过圆形轨道的最高点,做完整的圆周运动,则其不脱离轨道。
小球刚能通过最高点时,小球在最高点与轨道没有相互作用,重力提供向心力。
根据牛顿第二定律:![]()
小球由C运动到圆形轨道的最高点,机械能守恒:![]()
得:![]() ,即轨道半径不能超过1.08m。
,即轨道半径不能超过1.08m。
②若小球没有到达圆形轨道的与圆心等高处速度就减小到零,此后又沿轨道滑下,则其也不脱离轨道。
此过程机械能守恒,小球由C到达刚与圆心等高处,有:![]()
得:![]() ,即轨道半径不能小于2.7m。
,即轨道半径不能小于2.7m。
③若圆形轨道半径太大,就会与倾斜轨道相交,故圆形轨道半径最大时恰遇倾斜轨道相切。
当圆轨道与AB相切时,由几何关系得:![]() ,即圆轨道的半径不能超过1.5m。
,即圆轨道的半径不能超过1.5m。
综上所述,要使小球不离开轨道,R应该满足的条件是:![]() 。
。

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
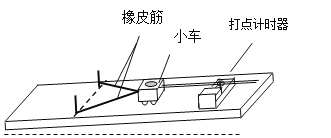
优秀生快乐假期每一天全新寒假作业本系列答案【题目】某实验小组采用如图所示的装置探究功与速度的关系,小车在橡皮筋的作用下弹出后,沿木板滑行。打点计时器工作频率为50Hz。 实验中木板略微倾斜,这样做 。
A.是为了使释放小车后,小车能匀加速下滑 |
B.是为了增大小车下滑的加速度 |
C.可使得橡皮筋做的功等于合外力对小车做的功 |
D.可使得橡皮筋松弛后小车做匀速运动 |
【题目】在《验证机械能守恒定律》的实验中。
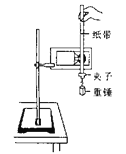
(1)下列实验操作顺序正确合理的一项是 (填序号)
A.先将固定在重物上的纸带穿过打点计时器,再将打点计时器固定在铁架台上 |
B.先用手提着纸带,使重物静止在打点计时器下方,再接通电源 |
C.先放开纸带让重物下落,再接通打点计时时器的电源 |
D.先取下固定在重物上的打好点的纸带,再切断打点计器的电源 |
(2)已知打点计时器所用电源的频率为50Hz,查得当地的重力加速度
g =9.8m/s2,测得所用的重物的质量1.00kg,实验中得到一条点迹清晰的纸带,如图,把第一个点记作O,另选连续的4个点A,B,C,D作为测量的点,经测量知道A,B,C,D个点到O点的距离分别为62.99cm,70.18cm,77.70cm,85.73cm.根据以上数据,可知重物由O点运动到C点,重力势能的减少等于____ _ J,动能增加量等于____ _ J。 (计算结果留三位有效数字)
实验结论是