题目内容
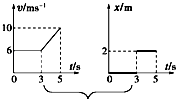
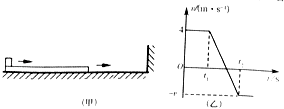
【题目】一长木板置于粗糙水平地面上,木板左端放置一小物块;在木板右方有一墙壁,木板右端与墙壁的距离为4.5m,如图(a)所示.t=0时刻开始,小物块与木板一起以共同速度向右运动,直至t=1s时木板与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板.已知碰撞后1s时间内小物块的v﹣t图线如图(b)所示.木板的质量是小物块质量的15倍,重力加速度大小g取10m/s2 . 求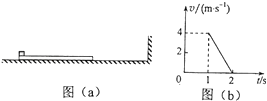
(1)木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2;
(2)木板的最小长度;
(3)木板右端离墙壁的最终距离.
【答案】
(1)
解:规定向右为正方向.木板与墙壁相碰前,小物块和木板一起向右做匀变速运动,设加速度为a1,小物块和木板的质量分别为m和M.由牛顿第二定律有﹣μ1(m+M)g=(m+M)a1 ①
由图可知,木板与墙壁碰前瞬间速度v1=4m/s,由运动学公式得
v1=v0+at ②
![]() ③
③
式中,t1=1s,s0=4.5m是木板碰前的位移,v0是小木块和木板开始运动时的速度.
联立①②③式和题给条件得 μ1=0.1 ④
在木板与墙壁碰撞后,木板以﹣v1的初速度向左做匀变速运动,小物块以v1的初速度向右做匀变速运动.设小物块的加速度为a2,由牛顿第二定律有﹣μ2mg=ma2 ⑤
由图可得 ![]() ⑥
⑥
式中,t2=2s,v2=0,联立⑤⑥式和题给条件得 μ2=0.4 ⑦
(2)
解:设碰撞后木板的加速度为a3,经过时间△t,木板和小物块刚好具有共同速度v3.由牛顿第二定律及运动学公式得
μ2mg+μ1(M+m)g=Ma3 ⑧
v3=﹣v1+a3△t ⑨
v3=v1+a2△t ⑩
碰撞后至木板和小物块刚好达到共同速度的过程中,木板运动的位移为 ![]() (11)
(11)
小物块运动的位移为 ![]() (12)
(12)
小物块相对木板的位移为△s=s2﹣s1(13)
联立⑥⑧⑨⑩(11)(12)(13)式,并代入数值得△s=6.0m
因为运动过程中小物块没有脱离木板,所以木板的最小长度应为6.0m.(14)
(3)
解:在小物块和木板具有共同速度后,两者向左做匀变速运动直至停止,设加速度为a4,此过程中小物块和木板运动的位移s3.由牛顿第二定律及运动学公式得 μ1(m+M)g=(m+M)a4 (15)
![]() (16)
(16)
碰后木板运动的位移为 s=s1+s3 (17)
联立⑥⑧⑨⑩(11)(15)(16)(17)式,并代入数值得 s=﹣6.5m (18)
木板右端离墙壁的最终距离为6.5m
【解析】(1)对碰前过程由牛顿第二定律时进行分析,结合运动学公式可求得μ1;再对碰后过程分析同理可求得μ2 . (2)分别对木板和物块进行分析,由牛顿第二定律求解加速度,由运动学公式求解位移,则可求得相对位移,即可求得木板的长度;(3)对木板和物块达相同静止后的过程进行分析,由牛顿第二定律及运动学公式联立可求得位移;则可求得木板最终的距离.