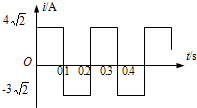
��Ŀ����
8������Ϊm��С����һ������ϵ��O�㣬����ֱƽ�������뾶ΪR��Բ���˶���С����ߵ�ʱ���ٶ�Ϊv1��������͵�ʱ���ٶȱ�Ϊv2�������ٶȴ�С�Ĺ�ϵΪv2=$\sqrt{4gR+{{v}_{1}}^{2}}$��������| A�� | ��͵���ٶȵ���СֵΪ$\sqrt{4gR}$ | |
| B�� | ��͵���ٶȵ���СֵΪ$\sqrt{5gR}$ | |
| C�� | ��͵����ߵ�ϸ�������IJ�ֵ��6mg | |
| D�� | ��͵����ߵ�ϸ�������IJ�ֵ��5mg |
���� ����Բ���˶�������ߵ���ٶ���Сʱ��������͵�ʱ�ٶ���С������ߵ㣬�������ṩ������ʱ���ٶ���С��������������ʽ��ʽ��
����Բ���˶�������ߵ㵽��͵�Ĺ����У����ݶ��ܶ�����ʽ������⣬����ߵ����͵������������ʽ��ʽ������ӵ��������Ӷ������͵����ߵ�ϸ�������IJ�ֵ��
��� �⣺A������Բ���˶�������ߵ���ٶ���Сʱ��������͵�ʱ�ٶ���С������ߵ㣬�������ṩ������ʱ���ٶ���С�����У�
$mg=m\frac{{{v}_{1}}^{2}}{R}$
��ã�${v}_{1}=\sqrt{gR}$��
����Բ���˶�������ߵ㵽��͵�Ĺ����У����ݶ��ܶ����ã�
$\frac{1}{2}m{{v}_{2}}^{2}-\frac{1}{2}m{{v}_{1}}^{2}=mg•2R$
��ã�${v}_{2}=\sqrt{5gR}$����A����B��ȷ��
C������ߵ㣬������������ʽ�ã�
${T}_{1}+mg=m\frac{{{v}_{1}}^{2}}{R}$
����͵㣬������������ʽ�ã�
${T}_{2}-mg=m\frac{{{v}_{2}}^{2}}{R}$
��ã�T2-T1=6mg����C��ȷ��D����
��ѡ��BC
���� �˵�ģ�ͺ�����ģ�����ڸ��г����������ֻ���ģ�ͣ�������ģ�Ͳ�һ����������ߵ���ٶȿ���Ϊ�㣬��������ߵ�ʱ���ٶȱ�����ڻ������С�ٶ�

| A�� | �����ʱ�䲻ͬ | B�� | ��ص��ٶȲ�ͬ | ||
| C�� | ����ļ��ٶ���ͬ | D�� | ���ʱ�������ܵı仯����ͬ |
 ��ͼ��ʾ��һ������ת���İ뾶Ϊr��ˮƽԲ���Ϸ�������ľ�飬ľ��M����Բ�̵ı�Ե����ľ��N������Բ��$\frac{1}{3}$r����ľ��M��N����֮��Ϊ1��3������Բ��Ħ��������ȣ����Ƕ���Բ��һ��������Բ���˶�������˵������ȷ���ǣ�������
��ͼ��ʾ��һ������ת���İ뾶Ϊr��ˮƽԲ���Ϸ�������ľ�飬ľ��M����Բ�̵ı�Ե����ľ��N������Բ��$\frac{1}{3}$r����ľ��M��N����֮��Ϊ1��3������Բ��Ħ��������ȣ����Ƕ���Բ��һ��������Բ���˶�������˵������ȷ���ǣ�������| A�� | M��N��ľ������ٶȴ�С��� | |
| B�� | M����Ħ����С��N���ܵ�Ħ���� | |
| C�� | M�����ļ��ٶ���N��3�� | |
| D�� | ��Բ���˶��ӿ죬N�����Բ���ȷ�������˶� |
| A�� | ˫��ϵͳ�Ĺ��Բ�Ļ������հ��ǿ��� | |
| B�� | ����������������һ����С | |
| C�� | ������������������䣬˫��ϵͳ�������ڻ�������������� | |
| D�� | ������������������䣬˫��ϵͳ�������ڻ������������С |

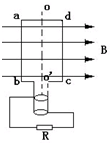 ��ͼ��ʾ��ab=25cm��ad=20cm������Ϊ50�ѵľ�����Ȧ����Ȧ�ܵ���r=1�����·����R=9�����Ÿ�Ӧǿ��B=0.4T����Ȧ�ƴ�ֱ�ڴŸ��ߵ�OO�����Խ��ٶ�50rad/s����ת������
��ͼ��ʾ��ab=25cm��ad=20cm������Ϊ50�ѵľ�����Ȧ����Ȧ�ܵ���r=1�����·����R=9�����Ÿ�Ӧǿ��B=0.4T����Ȧ�ƴ�ֱ�ڴŸ��ߵ�OO�����Խ��ٶ�50rad/s����ת������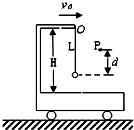 ��ͼ��ʾ���⻬ˮƽ�����и����й̶���˵�С������һ��L=0.80m������һ�˹̶�����˵Ķ˵�O����һ������һ����m=0.10kg��С������O��С���ϱ���ľ���ΪH=1.00m����ʼʱС����ͬС��һ����ˮƽ����������ֱ���˶����ٶȴ�Сv0=4m/s�����˶���������������һ����Ե��澲ֹ�Ķ���P����g=10m/s2��
��ͼ��ʾ���⻬ˮƽ�����и����й̶���˵�С������һ��L=0.80m������һ�˹̶�����˵Ķ˵�O����һ������һ����m=0.10kg��С������O��С���ϱ���ľ���ΪH=1.00m����ʼʱС����ͬС��һ����ˮƽ����������ֱ���˶����ٶȴ�Сv0=4m/s�����˶���������������һ����Ե��澲ֹ�Ķ���P����g=10m/s2�� ��ͼ��ʾ���ڹ⻬ˮƽ���ϵ���������ΪmA��mB������A��B����B�㹻������A��B��Ķ�Ħ������Ϊ�̣�����Ϊm��С����ˮƽ�ٶ�v����A����$\frac{v}{5}$���ٶȵ��أ���A��B��Ծ�ֹ����ٶ�Ϊ$\frac{6mv}{5��{m}_{A}+{m}_{B}��}$��
��ͼ��ʾ���ڹ⻬ˮƽ���ϵ���������ΪmA��mB������A��B����B�㹻������A��B��Ķ�Ħ������Ϊ�̣�����Ϊm��С����ˮƽ�ٶ�v����A����$\frac{v}{5}$���ٶȵ��أ���A��B��Ծ�ֹ����ٶ�Ϊ$\frac{6mv}{5��{m}_{A}+{m}_{B}��}$��