题目内容
13.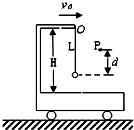 如图所示,光滑水平面内有个带有固定弯杆的小车,将一长L=0.80m的轻绳一端固定在弯杆的端点O,另一端连接一质量m=0.10kg的小球,悬点O到小车上表面的距离为H=1.00m.开始时小车连同小球一起在水平面上做匀速直线运动,速度大小v0=4m/s.在运动过程中轻绳碰到一个相对地面静止的钉子P.(g=10m/s2)
如图所示,光滑水平面内有个带有固定弯杆的小车,将一长L=0.80m的轻绳一端固定在弯杆的端点O,另一端连接一质量m=0.10kg的小球,悬点O到小车上表面的距离为H=1.00m.开始时小车连同小球一起在水平面上做匀速直线运动,速度大小v0=4m/s.在运动过程中轻绳碰到一个相对地面静止的钉子P.(g=10m/s2)(1)若轻绳碰到钉子时立刻断裂,且轻绳断裂前后小车的速度认为不变.从绳子断裂开始到小球落在小车上表面的过程中,小车前进的距离?
(2)若轻绳所能承受的最大拉力Fm=9.0N,要使碰钉子后瞬间细绳不被拉断,则钉子P到小球的距离d应满足什么条件?
(3)在(2)的情况下,试画出碰钉子后瞬间轻绳拉力F与钉子到小球的距离d间的关系图象.(标出特殊点的具体数值,但不需要写出计算过程)
分析 (1)绳子断裂后,小球相对于地面做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,小车做匀速直线运动,据此即可解答;
(2)绳子碰到钉子后做圆周运动,当绳子的拉力达到最大拉力时,绳子断裂,根据向心力公式列式即可求解.
(3)根据上题的结果分析F与d的倒数关系,从而作出F-$\frac{1}{d}$图象.
解答 解:(1)绳子断裂后,小球相对于地面做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,则哟:
$H-L=\frac{1}{2}g{t^2}$
s=v0t
联立解得:s=0.8m
(2)绳子碰到钉子后做圆周运动,当绳子的拉力达到最大拉力时,绳子断裂,则有:${F_m}-mg=m\frac{v_0^2}{d}$
解得:d=0.2m
故钉子P到小球的距离d应满足的条件是:0.2m≤d<0.8m
(3)结合上题的结论,作出F-$\frac{1}{d}$图象如下.
答:
(1)小车前进的距离为0.8m.
(2)钉子P到小球的距离d应满足的条件是:0.2m≤d<0.8m.
(3)作出F-$\frac{1}{d}$图象如上图所示.
点评 本题主要考查了平抛运动基本公式及向心力公式的直接应用,知道绳子断裂后,小球相对于地面做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动.

练习册系列答案
相关题目
3.下列关于时刻或时间的说法中,表示时刻的是( )
| A. | 列车在武昌站停车10分钟 | |
| B. | 第3s内 | |
| C. | 第3s末 | |
| D. | 列车从广州东站到北京站运行约22小时 |
4.平抛运动中,关于重力做功,下列说法正确的是( )
| A. | 重力不做功 | B. | 重力做功与路径无关 | ||
| C. | 重力做正功,机械能守恒 | D. | 重力做正功,机械能减少 |
8.质量为m的小球,用一根轻绳系在O点,在竖直平面内做半径为R的圆周运动,小球到达最高点时的速度为v1,到达最低点时的速度变为v2,两点速度大小的关系为v2=$\sqrt{4gR+{{v}_{1}}^{2}}$,则( )
| A. | 最低点的速度的最小值为$\sqrt{4gR}$ | |
| B. | 最低点的速度的最小值为$\sqrt{5gR}$ | |
| C. | 最低点和最高点细绳张力的差值是6mg | |
| D. | 最低点和最高点细绳张力的差值是5mg |
18.A、B两船的质量均为M,它们都静止在平静的湖面上,当A船上质量为$\frac{M}{2}$的人以水平速度v从A船跳到B船,再从B船跳回A船.设水对船的阻力不计,经多次跳跃后,人最终跳到B船上,则( )
| A. | A、B两船的速度大小之比为3:2 | |
| B. | A、B(包括人)动量大小之比为1:1 | |
| C. | A、B(包括人)动量之和为零 | |
| D. | 因跳跃次数未知,故以上答案均无法确定 |
8.关于匀速圆周运动,以下说法正确的是( )
| A. | 匀速圆周运动是匀速运动 | |
| B. | 匀速圆周运动是匀变速曲线运动 | |
| C. | 匀速圆周运动v、ω、T、f都是恒量 | |
| D. | 匀速圆周运动ω、T、f都是恒量,v方向时刻改变 |
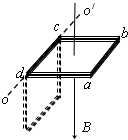 如图所示,匀强磁场竖直向下,磁感应强度为B.有一边长为L的正方形导线框abcd,匝数为N,可绕OO′边转动,导线框总质量为m,总电阻为R.现将导线框从水平位置由静止释放,不计摩擦,转到竖直位置时动能为Ek,则在此过程中流过导线某一截面的电量为$\frac{NB{L}^{2}}{R}$;导线框重力势能减少量为$\frac{1}{2}mgL$导线框中产生热量为$\frac{1}{2}mgL$-EK.
如图所示,匀强磁场竖直向下,磁感应强度为B.有一边长为L的正方形导线框abcd,匝数为N,可绕OO′边转动,导线框总质量为m,总电阻为R.现将导线框从水平位置由静止释放,不计摩擦,转到竖直位置时动能为Ek,则在此过程中流过导线某一截面的电量为$\frac{NB{L}^{2}}{R}$;导线框重力势能减少量为$\frac{1}{2}mgL$导线框中产生热量为$\frac{1}{2}mgL$-EK. 在“用油膜法估测分子大小”的实验中,所用的油酸酒精溶液的浓度为每1 000mL溶液中有纯油酸0.6mL,用注射器测得1mL上述溶液为80滴,把1滴该溶液滴入盛水的浅盘内,让油膜在水面上尽可能散开,测得油酸薄膜的轮廓形状和尺寸如图所示,图中单个正方形方格的边长为1cm.
在“用油膜法估测分子大小”的实验中,所用的油酸酒精溶液的浓度为每1 000mL溶液中有纯油酸0.6mL,用注射器测得1mL上述溶液为80滴,把1滴该溶液滴入盛水的浅盘内,让油膜在水面上尽可能散开,测得油酸薄膜的轮廓形状和尺寸如图所示,图中单个正方形方格的边长为1cm.