题目内容
20. 如图所示,在光滑水平面上叠放着质量为mA与mB的物体A和B(设B足够长),A与B间的动摩擦因数为μ,质量为m的小球以水平速度v射向A,以$\frac{v}{5}$的速度弹回,则A与B相对静止后的速度为$\frac{6mv}{5({m}_{A}+{m}_{B})}$.
如图所示,在光滑水平面上叠放着质量为mA与mB的物体A和B(设B足够长),A与B间的动摩擦因数为μ,质量为m的小球以水平速度v射向A,以$\frac{v}{5}$的速度弹回,则A与B相对静止后的速度为$\frac{6mv}{5({m}_{A}+{m}_{B})}$.
分析 小球与A碰撞过程,对小球和A组成的系统由动量守恒定律列出等式,对A与B组成的系统由动量守恒定律求解两者相对静止后的速度.
解答 解:小球与A碰撞过程,取向右为正方向,对小球和A组成的系统由动量守恒定律,有
mv=m(-$\frac{v}{5}$)+mAvA ①
设A和B相对静止后的速度为v,对A与B组成的系统由动量守恒定律,有
mAvA=(mA+mB)v′②
由①②得 v′=$\frac{6mv}{5({m}_{A}+{m}_{B})}$
故答案为:$\frac{6mv}{5({m}_{A}+{m}_{B})}$.
点评 对于物块在小车上运动的类型,动量往往守恒,有时还用到能量守恒求解.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 匀速圆周运动是速度不变的运动 | |
| B. | 平抛运动在相同时间内速度变化相同 | |
| C. | 当物体做曲线运动时,所受的合外力一定变化 | |
| D. | 匀速圆周运动是匀变速运动 |
8.质量为m的小球,用一根轻绳系在O点,在竖直平面内做半径为R的圆周运动,小球到达最高点时的速度为v1,到达最低点时的速度变为v2,两点速度大小的关系为v2=$\sqrt{4gR+{{v}_{1}}^{2}}$,则( )
| A. | 最低点的速度的最小值为$\sqrt{4gR}$ | |
| B. | 最低点的速度的最小值为$\sqrt{5gR}$ | |
| C. | 最低点和最高点细绳张力的差值是6mg | |
| D. | 最低点和最高点细绳张力的差值是5mg |
15.一位质量为m的运动员从下蹲状态向上起跳,经△t时间,身体伸直并刚好离开地面,速度为v,在此过程中( )
| A. | 地面对他的冲量为mv+mg△t | B. | 地面对他的冲量为mv-mg△t | ||
| C. | 地面对他做的功为$\frac{1}{2}$mv2 | D. | 地面对他做的功为零 |
15. 一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直平面内作半径为R的圆周运动,如图所示,则( )
一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直平面内作半径为R的圆周运动,如图所示,则( )
 一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直平面内作半径为R的圆周运动,如图所示,则( )
一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直平面内作半径为R的圆周运动,如图所示,则( )| A. | 小球过最高点时,杆所受弹力可以为零 | |
| B. | 小球过最高点时的最小速度是$\sqrt{gR}$ | |
| C. | 小球过最高点时,杆对球的作用力可以与球所受重力方向相反,此时重力一定大于杆对球的作用力 | |
| D. | 小球过最高点时,杆对球的作用力一定跟小球所受重力的方向相反 |
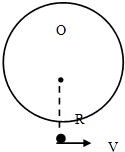 一质量m=1Kg的小球沿一光滑圆弧轨道滑下,经过圆弧最低点时速度大小为10m/s,已知圆弧轨道的半径R=5m,(g取10m/s2)求:
一质量m=1Kg的小球沿一光滑圆弧轨道滑下,经过圆弧最低点时速度大小为10m/s,已知圆弧轨道的半径R=5m,(g取10m/s2)求: 如图所示,竖直向上抛出质量为m的小球,小球上升的最大高度为h,上升和下降过程中,空气阻力的大小均为F,则从抛出至回到出发点的过程中,重力对小球做的功为多少?空气阻力对小球做的功为多少?
如图所示,竖直向上抛出质量为m的小球,小球上升的最大高度为h,上升和下降过程中,空气阻力的大小均为F,则从抛出至回到出发点的过程中,重力对小球做的功为多少?空气阻力对小球做的功为多少?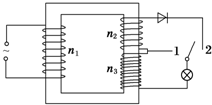 如图所示,一理想变压器的原线圈接在电压为220V的正弦交流电源上,两副线圈匝数分别为n2=16匝、n3=144匝,通过理想二极管、单刀双掷开关与一只“36V,18W”的灯泡相连(灯泡电阻不变),当开关接1时,灯泡正常发光,求
如图所示,一理想变压器的原线圈接在电压为220V的正弦交流电源上,两副线圈匝数分别为n2=16匝、n3=144匝,通过理想二极管、单刀双掷开关与一只“36V,18W”的灯泡相连(灯泡电阻不变),当开关接1时,灯泡正常发光,求