Question

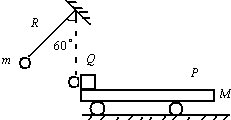
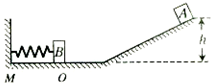
如图所示，斜面顶端距水平面高度为h，质量为m₁的小物块A从斜面顶端由静止滑下，进入水平滑道时无机械能损失，为使A制动，将轻弹簧的一端固定在水平滑道左端M处的墙上，另一端与质量为m₂挡板B相连，弹簧处于原长时，B恰位于滑道上的O点．A与B碰撞时间极短，碰后结合在一起共同压缩弹簧，已知在OM段A、B与水平面间的动摩擦因数均为μ，其余各处的摩擦不计，重力加速度为g，求
（1）物块A在与挡板B碰撞前瞬间速度v的大小；
（2）物块A在与挡板B碰撞后瞬间速度v 的大小；
（3）弹簧最大压缩量为d时的弹性势能Ep（设弹簧处于原长时弹性势能为零）．

Answer 1

（1）由机械能守恒定律，有m1gh=

1

2

m1v2
v=

2gh

（2）A、B在碰撞过程中内力远大于外力，由动量守恒，有m₁v=（m₁+m₂）v′
v′=

m1

m1+m2

v=

m1

m1+m2

2gh

．
（3）A、B克服摩擦力所做的功W=μ（m₁+m₂）gd
由能量守恒定律，有

1

2

(m1+m2)v′2=Ep+μ(m1+m2)gd
解得Ep=

m12gh

m1+m2

-μ(m1+m2)gd．
答：（1）物块 A在与挡板 B碰撞前瞬间速度 v的大小v=

2gh

．
（2）物块 A在与挡板 B碰撞后瞬间速度v的大小

m1

m1+m2

2gh

．
（3）弹簧最大压缩量为 d时的弹性势能Ep=

m12gh

m1+m2

-μ(m1+m2)gd．