题目内容
如图,竖直放置的斜面下端与光滑的圆弧轨道BCD的B端相切,圆弧半径为R,∠COB=q,斜面倾角也为q,现有一质量为m的小物体从斜面上的A点无初速滑下,且恰能通过光滑圆形轨道的最高点D.已知小物体与斜面间的动摩擦因数为m,求:

(1)AB长度l应该多大。
(2)小物体第一次通过C点时对轨道的压力多大。

(1)AB长度l应该多大。
(2)小物体第一次通过C点时对轨道的压力多大。
(1)  (2)
(2)
 (2)
(2)试题分析:

(1)因恰能过最高点D:
 ( 1) 2分
( 1) 2分 (2) 1分
(2) 1分物体从A运动到D全程,由动能定理:
 (3) 2分
(3) 2分 联立求得:
 2分
2分(2)物体从C运动到D的过程,设C点速度为
 ,由机械能守恒定律:
,由机械能守恒定律: (4 ) 2分
(4 ) 2分物体在C点时:
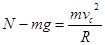 (5) 2分
(5) 2分联立求得:
 由牛顿第三定律可知,物体对轨道的压力是
由牛顿第三定律可知,物体对轨道的压力是 . 1分
. 1分点评:中等难度。解决此类问题的常规思路是利用机械能守恒求速度和竖直平面内合外力等于向心力求外力,但如果机械能不守恒,一般用动能定理求解。

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目



 37o。曲面所在区域和B点左下方的区域内都存在电场强度大小都为E的匀强电场,方向分别是水平向右和竖直向上。开始时有一质量为m的带电小球处于A点恰好保持静止。此后将曲面内的电场撤去,小球沿曲面下滑至B点时以速度V0水平抛出,最后落在电场内地面的P点,P点与B点间的水平距离为L。已知
37o。曲面所在区域和B点左下方的区域内都存在电场强度大小都为E的匀强电场,方向分别是水平向右和竖直向上。开始时有一质量为m的带电小球处于A点恰好保持静止。此后将曲面内的电场撤去,小球沿曲面下滑至B点时以速度V0水平抛出,最后落在电场内地面的P点,P点与B点间的水平距离为L。已知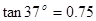 ,重力加速度为g。
,重力加速度为g。
 的圆弧轨道,O为圆心,OA水平,OB竖直,一小球从A点沿轨道射入,速度是v1,小球到达最高点B的速度是v2,则v1与v2比值可能是( )
的圆弧轨道,O为圆心,OA水平,OB竖直,一小球从A点沿轨道射入,速度是v1,小球到达最高点B的速度是v2,则v1与v2比值可能是( )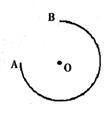
 : 1
: 1




 从A点出发,沿两个不同的轨道滑行分别到达C点或D点后水平抛出。已知两个轨道是固定的而且光滑,A、B、E在同一水平地面上, C、D、E在同一竖直线上,D点距地面的高度为h,C点高度为2h, 重力加速度为g。
从A点出发,沿两个不同的轨道滑行分别到达C点或D点后水平抛出。已知两个轨道是固定的而且光滑,A、B、E在同一水平地面上, C、D、E在同一竖直线上,D点距地面的高度为h,C点高度为2h, 重力加速度为g。
 ,并获得速度
,并获得速度 ,不计空气阻力,则在这个过程中( )
,不计空气阻力,则在这个过程中( )