题目内容
11.速度均为v0=90km/h的甲、乙两列火车,分别在同一水平面上的相邻的两条平行直线轨道上相向行驶.当它们相距l0=90km时,一只燕子以v1=150km/h的速度离开甲车的车头向乙车飞去,当它到达乙车的车头时又立即以原速率返回,并这样持续在两车头之间来回飞行,且燕子每次折返时的速度大小均不变,直到两车头相遇.在整个过程中,求:(1)这只燕子通过的路程L和位移大小s;
(2)这只燕子的平均速度大小$\overline{v}$.
分析 (1)两车相遇的时间内燕子都在飞行,根据速度时间关系求得燕了飞行的路程,燕子的位移与甲车的位移相同,据位移公式求得燕子的位移大小;
(2)根据平均速度公式求得燕子的平均速度大小.
解答 解:(1)根据题意得:
甲乙两车相距l0=v0t+v0t ①
燕子飞行的路程L=v1t ②
由①②两式代入数据解得:$L={v}_{1}\frac{{l}_{0}}{2{v}_{0}}$=$150×\frac{90}{2×90}km=75km$
燕子飞行的路程为75km
由题题意知,燕子的位移与甲车的位移相等
即x=${v}_{0}t=90×\frac{90}{2×90}km=45km$
(2)燕子飞行的平均速度$\overline{v}=\frac{x}{t}$ ③
代入数据解得:$\overline{v}=\frac{45}{\frac{1}{2}}km/h=90km/h$
答:(1)这只燕子通过的路程L为75km,位移大小s为45km;
(2)这只燕子的平均速度大小$\overline{v}$为90km/h.
点评 本题考查速度公式的灵活运用,关键燕子重复往返飞,只到两车相遇,燕子飞行的时间就等于两车相遇的时间.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.下列说法中正确的是( )
| A. | 场强的定义式E=$\frac{F}{q}$中,F是放入电场中的电荷所受的力,q是放入电场中的电荷的电量 | |
| B. | 场强的定义式E=$\frac{F}{q}$中,F是放入电场中的电荷所受的力,q是产生电场的电荷的电量 | |
| C. | 在库仑定律的表达式F=$\frac{k{q}_{1}{q}_{2}}{{r}^{2}}$中$\frac{k{q}_{2}}{{r}^{2}}$是电荷q2在q1处产生的场强大小,此场对q1作用的电场力F=q1×k$\frac{{q}_{2}}{{r}^{2}}$,同样k$\frac{{q}_{1}}{{r}^{2}}$是电荷q1产生的电场在点电荷q2处的场强的大小,此场对q2作用的电场力F=q2×k$\frac{{q}_{2}}{{r}^{2}}$ | |
| D. | 无论定义式E=$\frac{F}{q}$中的q值(不为零)如何变化,在电场中的同一点,F与q的比值始终不变 |
2. 如图所示电路中,电阻R1的阻值发生变化,而其他电阻的阻值都保持不变,发现电压表V3的示数减小,由此可以判定( )
如图所示电路中,电阻R1的阻值发生变化,而其他电阻的阻值都保持不变,发现电压表V3的示数减小,由此可以判定( )
 如图所示电路中,电阻R1的阻值发生变化,而其他电阻的阻值都保持不变,发现电压表V3的示数减小,由此可以判定( )
如图所示电路中,电阻R1的阻值发生变化,而其他电阻的阻值都保持不变,发现电压表V3的示数减小,由此可以判定( )| A. | 电压表V1的示数一定增大 | B. | 电压表V2的示数一定增大 | ||
| C. | 电阻R1的阻值一定增大 | D. | 电阻R1的阻值一定减小 |
9.某电场的电场线如图所示,电场中A、B两点的场强大小分别为EA和EB,由图可知( )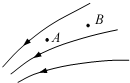

| A. | EA=EB | B. | EA>EB | C. | EA<EB | D. | 无法比较 |
 滑板运动是青年人喜爱的一种极限运动,其运动可抽象为:一个可以看做质点的小球,在如图所示的竖直平面内的光滑圆形轨道内的运动,圆的半径为R,在最低点A处放一小球,使小球获得水平速度$\sqrt{3.5gR}$起动,问小球能升到轨道什么位置?
滑板运动是青年人喜爱的一种极限运动,其运动可抽象为:一个可以看做质点的小球,在如图所示的竖直平面内的光滑圆形轨道内的运动,圆的半径为R,在最低点A处放一小球,使小球获得水平速度$\sqrt{3.5gR}$起动,问小球能升到轨道什么位置?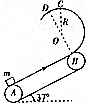 如图所示,传送带与两轮切点A、B间的距离为l=20m,半径为R=0.4m的光滑的半圆轨道与传送带相切于B点,C点为半圆轨道的最高点.BD为半圆轨道直径.物块质量为m=1kg.已知传送带与物块间的动摩擦因数=0.8,传送带与水平面夹角=37°.传送带的速度足够大,已知sin37°=0.6,cos37°=0.8,g=10ms2,物块可视为质点.求:
如图所示,传送带与两轮切点A、B间的距离为l=20m,半径为R=0.4m的光滑的半圆轨道与传送带相切于B点,C点为半圆轨道的最高点.BD为半圆轨道直径.物块质量为m=1kg.已知传送带与物块间的动摩擦因数=0.8,传送带与水平面夹角=37°.传送带的速度足够大,已知sin37°=0.6,cos37°=0.8,g=10ms2,物块可视为质点.求: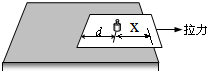 如图所示,将小砝码静置于桌面上的薄纸板上,砝码距纸板左边缘d=0.16m,距桌面右边缘x=0.3m.某时刻用水平向右的拉力将纸板以a1=4m/s2的加速度迅速抽出,此时砝码获得a2=2m/s2的加速度.若砝码的质量为m,各接触面间的动摩擦因数均为μ=0.2,重力加速度为g=10m/s2.求
如图所示,将小砝码静置于桌面上的薄纸板上,砝码距纸板左边缘d=0.16m,距桌面右边缘x=0.3m.某时刻用水平向右的拉力将纸板以a1=4m/s2的加速度迅速抽出,此时砝码获得a2=2m/s2的加速度.若砝码的质量为m,各接触面间的动摩擦因数均为μ=0.2,重力加速度为g=10m/s2.求