题目内容
2.跳伞运动员做低空跳伞表演,他离开飞机后先做自由落体运动,当距离地面125m时打开降落伞,伞张开后运动员就以9.9m/s2的加速度做匀减速直线运动,到达地面时速度为5m/s,(g=10m/s2)问:(1)运动员离开飞机时距地面的高度为多少?
(2)离开飞机后,运动员经过多少时间才能到达地面?
分析 (1)根据匀变速直线运动的速度位移公式求出打开降落伞时的速度,根据速度位移公式求出自由落体运动的位移,从而得出运动员离开飞机时距地面的高度.
(2)根据速度时间公式求出自由落体运动的时间和匀减速运动的时间,从而得出总时间.
解答 解:(1)根据速度位移公式得,${v}^{2}-{{v}_{0}}^{2}=2ax$,
解得${v}_{0}=\sqrt{{v}^{2}-2ax}$=$\sqrt{25+2×9.9×125}$m/s=50m/s,
则自由落体运动的位移${x}_{1}=\frac{{{v}_{0}}^{2}}{2g}=\frac{2500}{20}m=125m$,
运动员离开飞机距离地面的高度H=125+125m=250m.
(2)自由落体运动的时间${t}_{1}=\frac{{v}_{0}}{g}=\frac{50}{10}s=5s$,
匀减速运动的时间${t}_{2}=\frac{v-{v}_{0}}{a}=\frac{5-50}{-9.9}s≈4.55s$,
则t=t1+t2=5+4.5s=9.5s.
答:(1)运动员离开飞机时距地面的高度为250m.
(2)离开飞机后,运动员经过9.5s时间才能到达地面.
点评 解决本题的关键知道运动员在整个过程中的运动规律,结合匀变速直线运动的运动学公式灵活求解,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.电磁感应对社会贡献巨大,第一个发现电磁感应的科学家是( )
| A. | 奥斯特 | B. | 安培 | C. | 法拉第 | D. | 欧姆 |
10.在“探究小车速度随时间变化”的实验中,使用电磁打点计时器(所用交流电的频率为50Hz),得到如图所示的纸带,图中的点为计数点,相邻两计数点间还有四个点未画出来,下列表述正确的是( )


| A. | 实验时应先放开纸带再接通电源 | |
| B. | 由纸带可求出小车运动的加速度 | |
| C. | 由纸带可求出计数点B对应的速率 | |
| D. | 相邻两个计数点间的时间间隔为0.02s |
7. 如图,在与电容器连接的电路接通开关时,电源即给它充电,此平行板电容器由两块大小,形状完全相同的金属板平行放置构成,那么下列说法正确的是( )
如图,在与电容器连接的电路接通开关时,电源即给它充电,此平行板电容器由两块大小,形状完全相同的金属板平行放置构成,那么下列说法正确的是( )
 如图,在与电容器连接的电路接通开关时,电源即给它充电,此平行板电容器由两块大小,形状完全相同的金属板平行放置构成,那么下列说法正确的是( )
如图,在与电容器连接的电路接通开关时,电源即给它充电,此平行板电容器由两块大小,形状完全相同的金属板平行放置构成,那么下列说法正确的是( )| A. | 保持S闭合,减小两极板间的距离,则极板上的电荷量减小 | |
| B. | 保持S闭合,减小两极板间的距离,则极板上的电荷量增大 | |
| C. | 断开S,稍微增大两极板间的距离,则板间电场的电场强度增大 | |
| D. | 断开S,稍微减小两极板间的距离,则板间电场的电场强度减小 |
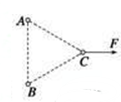 光滑绝缘的水平面上固定着三个带电小球A、B、C,它们的质量均为m,间距均为r,A、B带等量正电荷q,现对C球施一水平力F的同时,将三个小球都放开,如图所示,欲使得三个小球在运动过程中保持间距r不变,求:
光滑绝缘的水平面上固定着三个带电小球A、B、C,它们的质量均为m,间距均为r,A、B带等量正电荷q,现对C球施一水平力F的同时,将三个小球都放开,如图所示,欲使得三个小球在运动过程中保持间距r不变,求: 某高速公路边有如图所示的交通警示牌,其意义是指车辆的瞬时速度不得超过120km/h.若车辆驾驶员看到前车刹车后也相应刹车,反应时间是1s,假设车辆刹车的加速度相同,安全距离是两车不相碰所必须保持的距离2倍,则车辆行驶在这条公路上的安全距离是多少米?
某高速公路边有如图所示的交通警示牌,其意义是指车辆的瞬时速度不得超过120km/h.若车辆驾驶员看到前车刹车后也相应刹车,反应时间是1s,假设车辆刹车的加速度相同,安全距离是两车不相碰所必须保持的距离2倍,则车辆行驶在这条公路上的安全距离是多少米? 如图所示,重力G=10N的小球在竖直挡板作用下静止在倾斜面上,已知挡板也是光滑的,求:
如图所示,重力G=10N的小球在竖直挡板作用下静止在倾斜面上,已知挡板也是光滑的,求: