题目内容
1. 滑板运动是青年人喜爱的一种极限运动,其运动可抽象为:一个可以看做质点的小球,在如图所示的竖直平面内的光滑圆形轨道内的运动,圆的半径为R,在最低点A处放一小球,使小球获得水平速度$\sqrt{3.5gR}$起动,问小球能升到轨道什么位置?
滑板运动是青年人喜爱的一种极限运动,其运动可抽象为:一个可以看做质点的小球,在如图所示的竖直平面内的光滑圆形轨道内的运动,圆的半径为R,在最低点A处放一小球,使小球获得水平速度$\sqrt{3.5gR}$起动,问小球能升到轨道什么位置?
分析 小球刚离开轨道时,由重力的径向分力提供向心力,小球运动过程中机械能守恒,由牛顿第二定律和机械能守恒定律结合解答.
解答 解:设小球刚离开轨道时,其所在半径与竖直方向的夹角为θ.
则有 mgcosθ=m$\frac{{v}^{2}}{R}$
根据机械能守恒定律得:$\frac{1}{2}m{v}_{A}^{2}$=$\frac{1}{2}m{v}^{2}$+mgR(1+cosθ)
联立解得 cosθ=0.5,θ=60°
小球离开轨道时相对A点的高度为 h=R(1+cosθ)=1.5R
答:小球能升到轨道距离A点的高度为1.5R的位置.
点评 解决本题的关键是正确分析小球刚离开轨道时的向心力:重力的径向分力,利用牛顿第二定律求速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
 2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )| A. | 卫星“G1”和“G3”的加速度大小相等均为 $\frac{{R}^{2}}{r}$g | |
| B. | 卫星“G1”由位置A运动到位置B所需的时间为$\frac{2πr}{3R}$$\sqrt{\frac{r}{g}}$ | |
| C. | 如果调动“高分一号”卫星到达卫星“G3”所在的轨道,必须对其减速 | |
| D. | “高分一号”是低轨道卫星,其所在高度有稀薄气体,运行一段时间后,高度会降低,速度增大,机械能会减小 |
12.电磁感应对社会贡献巨大,第一个发现电磁感应的科学家是( )
| A. | 奥斯特 | B. | 安培 | C. | 法拉第 | D. | 欧姆 |
9.在“描绘小灯泡的伏安特性曲线”实验中,要测量一个标有“3V 1.5W”的灯泡两端的电压和通过它的电流,现有如下器材:
A.直流电源3V(内阻可不计)
B.直流电表0~3A(内阻约0.1Ω)
C.直流电表0~600mA(内阻约0.5Ω)
D.直流电压表0~3V(内阻约3kΩ)
E.直流电压表0~15V(内阻约200kΩ)
F.滑线变阻器(10Ω,1A)
G.滑线变阻器(1kΩ,300mA)

(1)除开关、导线外,为完成实验,需要从上述器材中选用ACDF(用字母).
(2)某同学用导线a、b、c、d、e、f、g和h连接的电路如图所示,电路中所有元器件都是完好的,且电压表和电流表已调零.闭合开关后发现电压表的示数为2V,电流表的示数为零,小灯泡不亮,则可判断断路的电线是d;若电压表示数为零,电流表的示数为0.3A,小灯泡亮,则断路的导线是h;若反复调节滑动变阻器,小灯泡亮度发生变化,但电压表、电流表示数不能调为零,则断路的导线是g.
(3)表中的各组数据是该同学在实验中测得的,某位同学根据表格中的数据作出了该灯泡的伏安特性曲线.
若将该灯泡与一个10Ω的定值电阻串联,直接接在题中电源两端,则可以估算出该灯泡的实际功率为0.19W.(结果保留两位有效数字)
A.直流电源3V(内阻可不计)
B.直流电表0~3A(内阻约0.1Ω)
C.直流电表0~600mA(内阻约0.5Ω)
D.直流电压表0~3V(内阻约3kΩ)
E.直流电压表0~15V(内阻约200kΩ)
F.滑线变阻器(10Ω,1A)
G.滑线变阻器(1kΩ,300mA)

(1)除开关、导线外,为完成实验,需要从上述器材中选用ACDF(用字母).
(2)某同学用导线a、b、c、d、e、f、g和h连接的电路如图所示,电路中所有元器件都是完好的,且电压表和电流表已调零.闭合开关后发现电压表的示数为2V,电流表的示数为零,小灯泡不亮,则可判断断路的电线是d;若电压表示数为零,电流表的示数为0.3A,小灯泡亮,则断路的导线是h;若反复调节滑动变阻器,小灯泡亮度发生变化,但电压表、电流表示数不能调为零,则断路的导线是g.
(3)表中的各组数据是该同学在实验中测得的,某位同学根据表格中的数据作出了该灯泡的伏安特性曲线.
| U/V | I/A |
| 0 | 0 |
| 0.5 | 0.17 |
| 1.0 | 0.30 |
| 1.5 | 0.39 |
| 2.0 | 0.45 |
| 2.5 | 0.49 |
16. 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带负电的质点仅在电场力作用下通过该区域时的运动轨迹,M,N是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带负电的质点仅在电场力作用下通过该区域时的运动轨迹,M,N是这条轨迹上的两点,据此可知( )
 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带负电的质点仅在电场力作用下通过该区域时的运动轨迹,M,N是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带负电的质点仅在电场力作用下通过该区域时的运动轨迹,M,N是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,a的电势最高 | |
| B. | 该质点在M点的电势能大于在N点的电势能 | |
| C. | 该质点在M点的动能大于在N点的动能 | |
| D. | 该质点在M点的加速度大于在N点的加速度 |
6.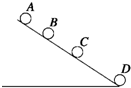 从斜面上某一位置每隔0.1s释放一个小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滑动的小球拍下如图所示的照片,测得xAB=15cm,xBC=20cm.小球的加速度和拍摄时小球B的速度分别为( )
从斜面上某一位置每隔0.1s释放一个小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滑动的小球拍下如图所示的照片,测得xAB=15cm,xBC=20cm.小球的加速度和拍摄时小球B的速度分别为( )
 从斜面上某一位置每隔0.1s释放一个小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滑动的小球拍下如图所示的照片,测得xAB=15cm,xBC=20cm.小球的加速度和拍摄时小球B的速度分别为( )
从斜面上某一位置每隔0.1s释放一个小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滑动的小球拍下如图所示的照片,测得xAB=15cm,xBC=20cm.小球的加速度和拍摄时小球B的速度分别为( )| A. | 30m/s2 3m/s | B. | 5m/s2 2$\sqrt{3}$m/s | C. | 5m/s2 1.75m/s | D. | 30m/s2 1.75m/s |
10.在“探究小车速度随时间变化”的实验中,使用电磁打点计时器(所用交流电的频率为50Hz),得到如图所示的纸带,图中的点为计数点,相邻两计数点间还有四个点未画出来,下列表述正确的是( )


| A. | 实验时应先放开纸带再接通电源 | |
| B. | 由纸带可求出小车运动的加速度 | |
| C. | 由纸带可求出计数点B对应的速率 | |
| D. | 相邻两个计数点间的时间间隔为0.02s |
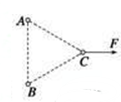 光滑绝缘的水平面上固定着三个带电小球A、B、C,它们的质量均为m,间距均为r,A、B带等量正电荷q,现对C球施一水平力F的同时,将三个小球都放开,如图所示,欲使得三个小球在运动过程中保持间距r不变,求:
光滑绝缘的水平面上固定着三个带电小球A、B、C,它们的质量均为m,间距均为r,A、B带等量正电荷q,现对C球施一水平力F的同时,将三个小球都放开,如图所示,欲使得三个小球在运动过程中保持间距r不变,求: