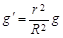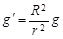题目内容
把水星和金星绕太阳的运动视为圆周运动。从水星与金星和太阳在一条直线上开始计时,若测得在相同时间内水星、金星转过的角度分别为θ1、θ2(均为锐角),则由此条件可求得水星和金星
| A.质量之比 |
| B.到太阳的距离之比 |
| C.绕太阳的动能之比 |
| D.受到的太阳引力之比 |
B
解析试题分析:已知相同时间内水星和金星转过的角度比,可求得角速度之比,根据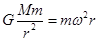 可求得它们到太阳的距离之比;因为水星和金星的质量关系未知,所以不能能求得它们绕太阳的动能之比和受太阳的引力之比;选项B 正确。
可求得它们到太阳的距离之比;因为水星和金星的质量关系未知,所以不能能求得它们绕太阳的动能之比和受太阳的引力之比;选项B 正确。
考点:万有引力定律的应用。

练习册系列答案
相关题目
在早期的反卫星试验中,攻击拦截方式之一是快速上升式攻击,即“拦截器”被送入与“目标卫星”轨道平面相同而高度较低的追赶轨道,然后通过机动飞行快速上升接近目标将“目标卫星”摧毁。图为追赶过程轨道示意图。下列叙述正确的是( )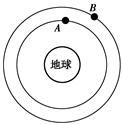
| A.图中A是“目标卫星”,B是“拦截器” |
| B.“拦截器”和“目标卫星”的绕行方向为图中的顺时针方向 |
| C.“拦截器”在上升的过程中重力势能会增大 |
| D.“拦截器”的加速度比“目标卫星”的加速度小 |
关于地球同步通讯卫星,下列说法中不正确的是
| A.它一定在赤道正上空运行 |
| B.各国发射的这种卫星轨道半径都一样 |
| C.它运行的线速度小于第一宇宙速度 |
| D.它运行的线速度介于第一和第二宇宙速度之间 |
某科学家估测一个密度约为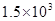 kg/m3的液态星球是否存在,他的主要根据之一就是它自转的周期,假若它存在,其自转周期的最小值约为( )(万有引力恒量G=6.67×10-11Nm2/kg2)
kg/m3的液态星球是否存在,他的主要根据之一就是它自转的周期,假若它存在,其自转周期的最小值约为( )(万有引力恒量G=6.67×10-11Nm2/kg2)
| A.104s | B.105s | C.2×104s | D.3×104s |
我国“玉兔号”月球车被顺利送抵月球表面,并发回大量图片和信息。若该月球车在地球表面的重力为 ,在月球表面的重力为
,在月球表面的重力为 。已知地球半径为
。已知地球半径为 ,月球半径为
,月球半径为 ,地球表面处的重力加速度为g,则
,地球表面处的重力加速度为g,则
A.“玉兔号”月球车在地球表面与月球表面质量之比为 |
B.地球的质量与月球的质量之比为 |
C.地球表面处的重力加速度与月球表面处的重力加速度之比为 |
D.地球的第一宇宙速度与月球的第一宇宙速度之比为 |
如图所示,轨道1是卫星绕地球运动的圆轨道,可以通过在A点加速使卫星在椭圆轨道2上运动。A点是近地点,B点是远地点。轨道1、2相切于A点。在远地点B加速后,可使卫星在圆轨道3上运动,轨道2、3相切于B点。则下列说法中正确的是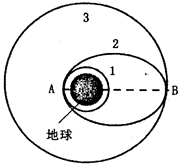
| A.卫星在轨道1上运行的速率大于在轨道2上经过B点时的速率 |
| B.无法比较卫星在轨道1上运行的速率和在轨道2上经过B点时的速率大小 |
| C.卫星在轨道2上经过A点时的向心加速度大于在轨道2上经过B点时的向心加速度 |
| D.卫星在轨道2上经过B点时的向心加速度小于在轨道3上运行时的向心加速度 |
如图所示,甲、乙两颗卫星以相同的轨道半径分别绕质量为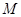 和
和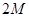 的行星做匀速圆周运动.下列说法正确的是
的行星做匀速圆周运动.下列说法正确的是 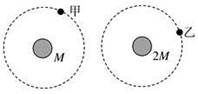
| A.甲的向心加速度比乙的小 |
| B.甲的运行周期比乙的小 |
| C.甲的角速度比乙的大 |
| D.甲的线速度比乙的大 |



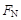 表示人对秤的压力,下面说法中正确的是
表示人对秤的压力,下面说法中正确的是