Question

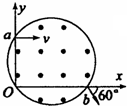
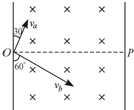
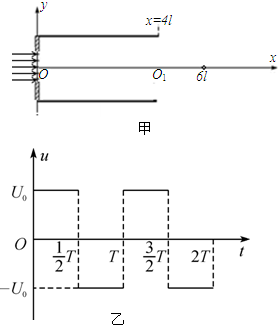
如图，A、B、C三板平行，B板延长线与圆切于P点，C板与圆切于Q点．离子源产生的初速为零、带电量为q、质量为m的正离子被电压为U₀的加速电场加速后沿两板间中点垂直射入匀强偏转电场，偏转后恰从B板边缘离开电场，经过一段匀速直线运动，进入半径为r的圆形匀强磁场，偏转后垂直C板打在Q点．（忽略粒子所受重力）
（

q

m

=2×104c/kg，U₀=100V，偏转电场极板长l=6cm、板间距d=2

3

cm，r=4cm）
求：（1）偏转电压U；
（2）粒子进入磁场时速度的大小及速度与B板的夹角；
（3）磁感应强度B的大小．

Answer 1

（1）电加速：qU₀=

1

2

mv₀²-0
电偏转：l=v₀t

d

2

=

1

2

at²
a=

qU

md

解得：U=

200

3

V
（2）电偏转：v_y=at
合速度大小为：v=

v02+vy2

=

4 3

3

×10³m/s
方向为：tanφ=

vy

v0

=

3

3

φ=30°
（3）由几何关系：R=rtan60°
洛伦兹力提供向心力：qvB=m

v2

R

解得：B=

5

3

T
答：（1）偏转电压U为

200

3

V；
（2）粒子进入磁场时速度的大小及速度与B板的夹角30°；
（3）磁感应强度B的大小

5

3

T．