��Ŀ����
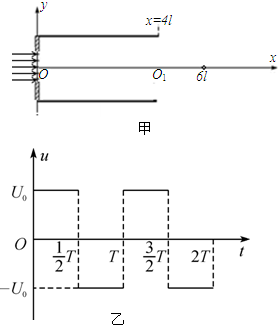
��ͼ����ʾ����ƽ�н�������Ϊ2l�����峤��Ϊ4l��������������ͼ����ʾ�Ľ����ѹ��t=0ʱ�ϼ�������磩���Լ�����������OO1Ϊx�Ὠ������ϵ������ƽ�а����������в��п���Ϊl�ĵ�������ƽ����x��ij��ٶ�v0��t=0ʱ��ͣ����������䣮��֪���Ӷ��ܴ��Ҳ��������������������x��ƽ�У����е���������������Ϊ2l����������Ϊm�������Ϊe�����Ե���֮������������
��1�����ѹ������T�͵�ѹU0�Ĵ�С��
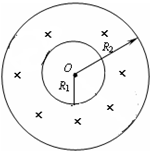
��2���ڵ糡������Ӵ�ֱֽ����н���ǿ�ų�����ʹ���е��Ӿ����н���ǿ�ų����ܻ���ڣ�6l��0���㣬�����Ӵų��Ÿ�Ӧǿ��B�����ֵ����Сֵ��
��3�����O������ĵ��Ӹճ�����ʱ�IJ���λ�ƣ�
��1�����ѹ������T�͵�ѹU0�Ĵ�С��
��2���ڵ糡������Ӵ�ֱֽ����н���ǿ�ų�����ʹ���е��Ӿ����н���ǿ�ų����ܻ���ڣ�6l��0���㣬�����Ӵų��Ÿ�Ӧǿ��B�����ֵ����Сֵ��
��3�����O������ĵ��Ӹճ�����ʱ�IJ���λ�ƣ�

��1�������ڵ糡��ˮƽ����������ֱ���˶���
��4l=v0nT����ã�T=
��n=1��2��3������
�����ڵ糡���˶�������λ�ƣ�
=2n?
a(
)2����ţ�ٵڶ����ɵã�a=
��
��ã�U0=
��n=1��2��3������
��2�������˶��켣��ͼ��ʾ��
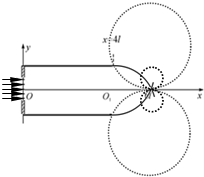
��ͼʾ��֪���������Բ�뾶���㣺rm2=(2l)2+(rm-l)2����ã�rm=2.5l��
���ڴ������ӵ��켣�뾶���ڴų�����뾶ʱ���������ӽ������һ�㣬
��ţ�ٵڶ����ɵã�qv0Bmin=
����ã�Bmin=
��
��С����Բ�뾶Ϊrn=0.5l��
��ţ�ٵڶ����ɵã�qv0Bmax=
����ã�Bmax=
��
��3����ʱ��Ϊ�ӣ�
���ӣ�0����t=kT+����(
���ӣ�0)ʱ���ӽ���糡��
��
������n=1��2��3����k=0��1��2��3������
��t=(k+
)T+����(
���ӣ�0)����糡
��y2=-n[
aT2-aT��]=
(t-kT-
T)-
=
-
l������n=1��2��3����k=0��1��2��3������
����������t=kT+����(T���ӣ�
)����糡ʱ�����糡���ܲ���Ϊ��
������n=1��2��3����k=0��1��2��3������
�����ⷨ����kT��t��kT+
����
������+y�����һ�μ��ٵ�ʱ��Ϊ
-(t-kT)
������-y�����һ�μ��ٵ�ʱ��Ϊt-kTy={
a[
-(t-kT)]2-
a(t-kT)2}?2n
��ã�y=
naT2-naTt������aT2=
��aT=
v0��
��y=
l-
nv0t��n=1��2��3����k=0��1��2��3����
��kT+
��t��kT+T����
������-y�����һ�μ��ٵ�ʱ��ΪT-��t-kT��
������+y�����һ�μ��ٵ�ʱ��Ϊt-kT-
y={-
a[T-(t-kT)]2+
a(t-kT-
)2}?2n
��ã�y=
naT2-naTt������aT2=
��aT=
v0����y=
nv0t-
l��n=1��2��3����k=0��1��2��3������
�𣺣�1�������ѹ������T=
��n=1��2��3��������ѹU0=
��n=1��2��3������
��2�����Ӵų��Ÿ�Ӧǿ��B�����ֵBmax=
����СֵBmin=
��
��3����O������ĵ��Ӹճ�����ʱ�IJ���λ��Ϊ
-
����n=1��2��3����k=0��1��2��3��������
-
l������n=1��2��3����k=0��1��2��3������
��4l=v0nT����ã�T=
| 4l |
| nv0 |
�����ڵ糡���˶�������λ�ƣ�
| l |
| 2 |
| 1 |
| 2 |
| T |
| 2 |
| eU0 |
| 2lm |
��ã�U0=
nm
| ||
| 4e |
��2�������˶��켣��ͼ��ʾ��

��ͼʾ��֪���������Բ�뾶���㣺rm2=(2l)2+(rm-l)2����ã�rm=2.5l��
���ڴ������ӵ��켣�뾶���ڴų�����뾶ʱ���������ӽ������һ�㣬
��ţ�ٵڶ����ɵã�qv0Bmin=
m
| ||
| rm |
| 2mv0 |
| 5el |
��С����Բ�뾶Ϊrn=0.5l��
��ţ�ٵڶ����ɵã�qv0Bmax=
m
| ||
| rn |
| 2mv0 |
| el |
��3����ʱ��Ϊ�ӣ�
| T |
| 2 |
| T |
| 2 |
��
|
��t=(k+
| 1 |
| 2 |
| T |
| 2 |
��y2=-n[
| 1 |
| 4 |
| nv0 |
| 2 |
| 1 |
| 2 |
| l |
| 2 |
| nv0t |
| 2 |
| (4k+3) |
| 2 |
����������t=kT+����(T���ӣ�
| T |
| 2 |
|
�����ⷨ����kT��t��kT+
| T |
| 2 |
������+y�����һ�μ��ٵ�ʱ��Ϊ
| T |
| 2 |
������-y�����һ�μ��ٵ�ʱ��Ϊt-kTy={
| 1 |
| 2 |
| T |
| 2 |
| 1 |
| 2 |
��ã�y=
| 4k+1 |
| 4 |
| 2l |
| n |
| 1 |
| 2 |
��y=
| 4k+1 |
| 2 |
| 1 |
| 2 |
��kT+
| T |
| 2 |
������-y�����һ�μ��ٵ�ʱ��ΪT-��t-kT��
������+y�����һ�μ��ٵ�ʱ��Ϊt-kT-
| T |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| T |
| 2 |
��ã�y=
| 4k+1 |
| 4 |
| 2l |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
| 4k+3 |
| 2 |
�𣺣�1�������ѹ������T=
| 4l |
| nv0 |
nm
| ||
| 4e |
��2�����Ӵų��Ÿ�Ӧǿ��B�����ֵBmax=
| 2mv0 |
| el |
| 2mv0 |
| 5el |
��3����O������ĵ��Ӹճ�����ʱ�IJ���λ��Ϊ
| (4k+1)l |
| 2 |
| nv0t |
| 2 |
| nv0t |
| 2 |
| (4k+3) |
| 2 |

��ϰ��ϵ�д�
�����Ŀ