题目内容
8.某汽车以初速度v0=14m/s制动后做匀减速直线运动,经3.5s后静止.(1)求汽车做匀减速直线运动的加速度大小.
(2)求汽车在静止前的1s内、2s内、3s内通过的位移之比.
(3)求汽车在制动后的第1s内、第2s内、第3s内通过的位移之比.
分析 (1)根据速度时间公式求出汽车做匀减速运动的加速度大小.
(2)采用逆向思维,结合位移时间公式求出静止前的1s内、2s内、3s内通过的位移之比.
(3)根据位移时间公式求出第1s内、第2s内、第3s内的位移,从而得出位移之比.
解答 解:(1)根据速度时间公式得,汽车匀减速运动的加速度大小为:
a=$\frac{{v}_{0}}{t}$=$\frac{14}{3.5}m/{s}^{2}=4m/{s}^{2}$.
(2)采用逆向思维,根据x=$\frac{1}{2}a{t}^{2}$知,汽车在静止前的1s内、2s内、3s内通过的位移之比为1:4:9.
(3)汽车制动后第1s内的位移为:
${x}_{1}={v}_{0}{t}_{1}-\frac{1}{2}a{{t}_{1}}^{2}$=$14×1-\frac{1}{2}×4×1m=12m$,
第2s内的位移为:
${x}_{2}={v}_{0}{t}_{2}-\frac{1}{2}a{{t}_{2}}^{2}-{x}_{1}$=$14×2-\frac{1}{2}×4×4-12$m=8m.
第3s内的位移为:
${x}_{3}={v}_{0}{t}_{3}-\frac{1}{2}a{{t}_{3}}^{2}-({v}_{0}{t}_{2}-\frac{1}{2}a{{t}_{2}}^{2})$=$14×3-\frac{1}{2}×4×9-(14×2-\frac{1}{2}×4×4)$m=4m,
则汽车在制动后的第1s内、第2s内、第3s内通过的位移之比为3:2:1.
答:(1)汽车做匀减速直线运动的加速度大小为4m/s2;
(2)汽车在静止前的1s内、2s内、3s内通过的位移之比为1:4:9.
(3)汽车在制动后的第1s内、第2s内、第3s内通过的位移之比为3:2:1.
点评 解决本题的关键掌握匀变速直线运动的运动学公式,并能灵活运用,注意逆向思维在运动学问题中的运用.

| A. | 仅由阿伏加德罗常数、气体的摩尔质量和密度,能估算该种气体分子大小 | |
| B. | 在绝热条件下压缩气体,气体的内能一定增加 | |
| C. | 一定质量的100℃水变成100℃的水蒸气,其分子势能相同 | |
| D. | 由于液体表面分子间距离大于液体内部分子间的距离,液面分子间表现为引力,所以液体表面具有收缩的趋势 | |
| E. | 封闭气体的密度变小,单位时间内打到器壁单位面积上的分子数减少,分子平均动能增加,气体的压强可能不变 |
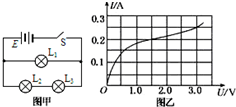 在如图甲所示的电路中,电源的电动势为3.0V,内阻不计,灯L1、L2、L3为三个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示.当开关闭合后,下列说法中正确的是( )
在如图甲所示的电路中,电源的电动势为3.0V,内阻不计,灯L1、L2、L3为三个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示.当开关闭合后,下列说法中正确的是( )| A. | 灯泡L1的电流为灯泡L2的电流2倍 | B. | 灯泡L1的电阻为1.2Ω | ||
| C. | 灯泡L2消耗的电功率为0.3W | D. | 灯泡L3消耗的电功率为0.75W |
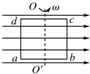 如图所示,一单匝矩形线圈abcd,已知ab边长为l1,bc边长为l2,在磁感应强度为B的匀强磁场中绕OO′轴以角速度ω从图示位置开始匀速转动,则t时刻线圈中的感应电动势为( )
如图所示,一单匝矩形线圈abcd,已知ab边长为l1,bc边长为l2,在磁感应强度为B的匀强磁场中绕OO′轴以角速度ω从图示位置开始匀速转动,则t时刻线圈中的感应电动势为( )| A. | 0.5Bl1l2ωsinωt | B. | 0.5Bl1l2ωcosωt | C. | Bl1l2ωsinωt | D. | Bl1l2ωcosωt |
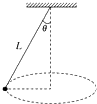 如图所示,一根长为L的轻质细绳上端固定,下端栓一个质量为m的小球,使小球子啊水平面内做匀速圆周运动,短绳与竖直方向夹角为θ,则下列说法正确的是( )
如图所示,一根长为L的轻质细绳上端固定,下端栓一个质量为m的小球,使小球子啊水平面内做匀速圆周运动,短绳与竖直方向夹角为θ,则下列说法正确的是( )| A. | 细绳的拉力大小为mgsinθ | B. | 小球的向心力为mgtanθ | ||
| C. | 小球的动能为$\frac{mgLtanθ}{2}$ | D. | 小球的角速度为$\sqrt{\frac{gtanθ}{L}}$ |