题目内容
17.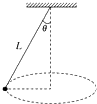 如图所示,一根长为L的轻质细绳上端固定,下端栓一个质量为m的小球,使小球子啊水平面内做匀速圆周运动,短绳与竖直方向夹角为θ,则下列说法正确的是( )
如图所示,一根长为L的轻质细绳上端固定,下端栓一个质量为m的小球,使小球子啊水平面内做匀速圆周运动,短绳与竖直方向夹角为θ,则下列说法正确的是( )| A. | 细绳的拉力大小为mgsinθ | B. | 小球的向心力为mgtanθ | ||
| C. | 小球的动能为$\frac{mgLtanθ}{2}$ | D. | 小球的角速度为$\sqrt{\frac{gtanθ}{L}}$ |
分析 小球只受重力和拉力作用,小球做圆周运动所需要的向心力是绳子拉力沿水平方向指向圆心的分力提供的,可以根据牛顿第二定律和向心力列式求出线速度和角速度,从而求出动能.
解答 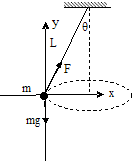 解:A、小球的受力分析如图所示,沿y轴方向有:
解:A、小球的受力分析如图所示,沿y轴方向有:
Fcosθ-mg=0
解得:F=$\frac{mg}{cosθ}$,故A错误;
B、向心力Fn=Fsinθ=mgtanθ,故B正确;
C、沿x轴方向:Fsinθ=m$\frac{{v}^{2}}{R}$
R=Lsinθ
解得:${E}_{K}=\frac{1}{2}m{v}^{2}=\frac{mgLtanθsinθ}{2}$,故C错误;
D、根据Fsinθ=mω2R
解得:$ω=\sqrt{\frac{gtanθ}{Lsinθ}}=\sqrt{\frac{g}{Lcosθ}}$,故D错误.
故选:B
点评 解决本题的关键搞清小球做圆周运动向心力的来源,运用牛顿第二定律进行求解,特别注意圆周运动的半径不是L,难度适中.

练习册系列答案
相关题目
7.以下说法中正确的是( )
| A. | 熵增加原理说明一切自然过程总是向着分子热运动的无序性减少的方向进行 | |
| B. | 在绝热条件下压缩气体,气体的内能一定增加 | |
| C. | 布朗运动是在显微镜中看到的液体分子的无规则运动 | |
| D. | 单晶体和多晶体的物理性质是各向异性的,非晶体是各向同性的 |
5.汽车进行刹车试验:按规定速率8m/s行驶的汽车,刹车后拖行距离不得超过5.9m,若速率从8m/s匀减速至零,用时1s.那么对上述刹车试验的拖行距离的计算及是否符合规定的判断正确的是( )
| A. | 拖行距离为8m,符合规定 | B. | 拖行距离为8m,不符合规定 | ||
| C. | 拖行距离为4m,符合规定 | D. | 拖行距离为4m,不符合规定 |
12.关于平抛运动,下列说法正确的是( )
| A. | 平抛运动的加速度是时刻变化的 | |
| B. | 平抛运动是非匀变速曲线运动 | |
| C. | 平抛运动的飞行时间决定于抛出时的高度 | |
| D. | 平抛运动的水平位移决定于初速度的大小 |
2.甲和乙是两颗人造地球卫星,甲的轨道半径较大,则下列说法正确的是( )
| A. | 甲的线速度一定大于7.9km/s | B. | 甲的周期较大 | ||
| C. | 乙的加速度较大 | D. | 乙的向心加速度较大 |
6. 如图电路中电源内阻忽略,R阻值与灯泡的电阻值相等,L的自感系数都很大,A、B为两个完全相同的灯泡,当S闭合时,下列说法正确的是( )
如图电路中电源内阻忽略,R阻值与灯泡的电阻值相等,L的自感系数都很大,A、B为两个完全相同的灯泡,当S闭合时,下列说法正确的是( )
 如图电路中电源内阻忽略,R阻值与灯泡的电阻值相等,L的自感系数都很大,A、B为两个完全相同的灯泡,当S闭合时,下列说法正确的是( )
如图电路中电源内阻忽略,R阻值与灯泡的电阻值相等,L的自感系数都很大,A、B为两个完全相同的灯泡,当S闭合时,下列说法正确的是( )| A. | A比B先亮,然后A灭 | B. | B比A先亮,然后A逐渐变暗 | ||
| C. | B比A先亮,然后B逐渐变暗 | D. | A、B一起亮,然后B灭 |
7.自高为h的塔顶自由落下一物体a,与此同时物体b从塔底以初速度v0竖直向上抛,且a、b两物体在同一直线上运动,下列说法中正确的( )
| A. | 若v0>$\sqrt{gh}$则两物体在b上升过程中相遇 | |
| B. | 若v0=$\sqrt{gh}$则两物体在地面相遇 | |
| C. | 若$\sqrt{gh}$>v0>$\sqrt{\frac{gh}{2}}$则两物体在b下降途中相遇 | |
| D. | 若v0<$\sqrt{\frac{gh}{2}}$则两物体不可能在空中相遇 |