题目内容
【题目】如图所示,光滑水平平台AB与竖直光滑半圆轨道AC平滑连接,C点切线水平,长为L=4m的粗糙水平传送带BD与平台无缝对接。质量分别为m1=0.3kg和m2=1kg两个小物体中间有一被压缩的轻质弹簧,用细绳将它们连接。已知传送带以v0=1.5m/s的速度向左匀速运动,小物体与传送带间动摩擦因数为μ=0.15.某时剪断细绳,小物体m1向左运动,m2向右运动速度大小为v2=3m/s,g取10m/s2.求:
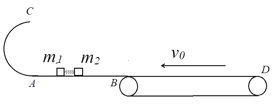
(1)剪断细绳前弹簧的弹性势能Ep
(2)从小物体m2滑上传送带到第一次滑离传送带的过程中,为了维持传送带匀速运动,电动机需对传送带多提供的电能E
(3)为了让小物体m1从C点水平飞出后落至AB平面的水平位移最大,竖直光滑半圆轨道AC的半径R和小物体m1平抛的最大水平位移x的大小。
【答案】(1)19.5J(2)6.75J(3)R=1.25m时水平位移最大为x=5m
【解析】
(1)对m1和m2弹开过程,取向左为正方向,由动量守恒定律有:
0=m1v1-m2v2
解得
v1=10m/s
剪断细绳前弹簧的弹性势能为:
![]()
解得
Ep=19.5J
(2)设m2向右减速运动的最大距离为x,由动能定理得:
-μm2gx=0-![]() m2v22
m2v22
解得
x=3m<L=4m
则m2先向右减速至速度为零,向左加速至速度为v0=1.5m/s,然后向左匀速运动,直至离开传送带。
设小物体m2滑上传送带到第一次滑离传送带的所用时间为t。取向左为正方向。
根据动量定理得:
μm2gt=m2v0-(-m2v2)
解得:
t=3s
该过程皮带运动的距离为:
x带=v0t=4.5m
故为了维持传送带匀速运动,电动机需对传送带多提供的电能为:
E=μm2gx带
解得:
E=6.75J
(3)设竖直光滑轨道AC的半径为R时小物体m1平抛的水平位移最大为x。从A到C由机械能守恒定律得:
![]()
由平抛运动的规律有:
x=vCt1![]()
联立整理得
![]()
根据数学知识知当
4R=10-4R
即R =1.25m时,水平位移最大为
x=5m

 初中学业考试导与练系列答案
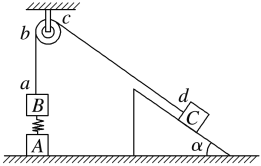
初中学业考试导与练系列答案【题目】如图所示,足够长的光滑平行导轨MN、PQ倾斜放置,两导轨间距离为![]() ,导轨平面与水平面间的夹角为
,导轨平面与水平面间的夹角为![]() ,磁感应强度为B的匀强磁场垂直于导轨平面向上,导轨的M、P两端连接阻值为
,磁感应强度为B的匀强磁场垂直于导轨平面向上,导轨的M、P两端连接阻值为![]() 的电阻,金属棒ab垂直于导轨放置并用细线通过光滑定滑轮与重物相连,金属棒ab的质量
的电阻,金属棒ab垂直于导轨放置并用细线通过光滑定滑轮与重物相连,金属棒ab的质量![]() ,电阻
,电阻![]() ,重物的质量
,重物的质量![]() ,如果将金属棒和重物由静止释放,金属棒沿斜面上滑的距离与时间的关系如表所示,不计导轨电阻,g取
,如果将金属棒和重物由静止释放,金属棒沿斜面上滑的距离与时间的关系如表所示,不计导轨电阻,g取![]() 求:
求:
时间t(s) | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
上滑距离(m) | 0 | 0.05 | 0.15 | 0.35 | 0.70 | 1.05 | 1.40 |
(1)ab棒最终做匀速直线运动的速度是多少?
(2)磁感应强度B的大小是多少?
(3)当金属棒ab的速度![]() 时,金属棒ab上滑的加速度大小是多少?
时,金属棒ab上滑的加速度大小是多少?