题目内容
8. 如图所示,一质量为m=1kg的小物块轻放在水平匀速运动的传送带上的A点,随传送带运动到B点,小物块从C点沿圆弧切线进入竖直光滑的半圆轨道恰能做圆周运动,已知圆弧半径R=1m,轨道最低点为D,D点距水平面的高度h=4.5m.小物块离开D点后恰好垂直碰击放在水平面上E点的固定倾斜挡板,倾斜挡板与水平面间的夹角θ=30°,已知小物块与传送带间的动摩擦因数μ=0.3,传送带以5m/s恒定速率顺时针转动,g=10m/s2.求:
如图所示,一质量为m=1kg的小物块轻放在水平匀速运动的传送带上的A点,随传送带运动到B点,小物块从C点沿圆弧切线进入竖直光滑的半圆轨道恰能做圆周运动,已知圆弧半径R=1m,轨道最低点为D,D点距水平面的高度h=4.5m.小物块离开D点后恰好垂直碰击放在水平面上E点的固定倾斜挡板,倾斜挡板与水平面间的夹角θ=30°,已知小物块与传送带间的动摩擦因数μ=0.3,传送带以5m/s恒定速率顺时针转动,g=10m/s2.求:(1)传送带AB两端的距离
(2)小物块经过E点时速度大小
(3)经过D点时对轨道的压力的大小.
分析 (1)小物块从C点沿圆弧切线进入竖直光滑的半圆轨道恰能做圆周运动,知物块对轨道的压力恰好为零,根据重力提供向心力求出C点的速度,再根据牛顿第二定律求出物块在传送带上运动的加速度,根据运动学公式求出传送带AB两端的距离.
(2)据平抛运动好速度的分解求出E点的速度.
(3)根据动能定理求出物块在D点的速度,再通过牛顿第二定律求出轨道对物块的支持力,从而得出物块对轨道的压力.
解答 解:(1)物块在C点恰好做圆周运动
所以mg=$\frac{m{v}_{c}^{2}}{R}$
解得:vc=$\sqrt{gR}$=$\sqrt{10}$m/s
因vc<5m/s,从A到C做匀加速直线运动
据牛顿第二定律得:μmg=ma
解得:a=μg=3m/s2
据运动学公式:xAB=$\frac{{v}_{c}^{2}}{2a}$
联立以上解得:$\frac{5}{3}m$
(2)从D到E做平抛运动,
到E点时,据运动的分解得:
竖直方向:vy=$\sqrt{2gh}$=$\sqrt{90}$m/s
又因为:θ=30°
联立以上解得:VE=$\frac{{v}_{y}}{cosθ}$=$\frac{\sqrt{90}}{\frac{\sqrt{3}}{2}}m/s$=2$\sqrt{30}$m/s
(3)D点速度与平抛运动水平方向速度相等
ND-mg=$\frac{m{v}_{x}^{2}}{R}$
代入数据解得:ND=40N
根据牛顿第三定律,经过D点时对轨道的压力大小为40N
答:(1)传送带AB两端的距离$\frac{5}{3}m$.
(2)小物块经过E点时速度大小2$\sqrt{30}$m/s
(3)经过D点时对轨道的压力的大小40N.
点评 解决本题的关键理清物块的运动,物块经历了匀加速直线运动,圆周运动和平抛运动,根据牛顿第二定律、动能定理以及运动学公式综合求解.

| A. | $\sqrt{3}$:1 | B. | 1:1 | C. | 1:$\sqrt{2}$ | D. | $\sqrt{2}$:1 |
 如图所示,在足够长的斜面上A点,以水平速度v0抛出一个小球,不计空气阻力,它落到斜面上的水平距离为x1;若将此球改用2v0水平速度抛出,落到斜面上的水平距离为x2,则x1:x2为( )
如图所示,在足够长的斜面上A点,以水平速度v0抛出一个小球,不计空气阻力,它落到斜面上的水平距离为x1;若将此球改用2v0水平速度抛出,落到斜面上的水平距离为x2,则x1:x2为( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
| A. | 6N的拉力 | B. | 6N的压力 | C. | 24N的拉力 | D. | 54N的拉力 |
| A. | 两个直线运动的合运动一定是直线运动 | |
| B. | 两个匀速直线运动的合运动一定是直线运动 | |
| C. | 两个匀加速直线运动的合运动一定是直线运动 | |
| D. | 一个匀加速运动和一个匀速运动的合运动一定是直线运动 |
| A. | 物体A上抛的初速度和物体B落地时的速度大小相等,都是2v | |
| B. | 物体A和B在空中运动的时间相等 | |
| C. | 物体A上升的最大高度和物体B开始下落的高度相等 | |
| D. | 两物体在空中同时到达同一个高度处一定是物体B开始下落时的高度的一半 |
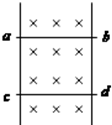 竖直放置的平行光滑金属导轨,其电阻不计,磁场方向如图所示,磁感应强度B=0.5T,有两根相同的导体棒ab及cd,长0.2m,电阻0.1Ω,重0.1N,现用力向上拉动导体ab,使之匀速上升(与导轨接触良好).此时cd恰好静止不动,求:
竖直放置的平行光滑金属导轨,其电阻不计,磁场方向如图所示,磁感应强度B=0.5T,有两根相同的导体棒ab及cd,长0.2m,电阻0.1Ω,重0.1N,现用力向上拉动导体ab,使之匀速上升(与导轨接触良好).此时cd恰好静止不动,求: