题目内容
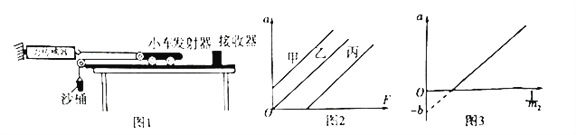
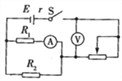
【题目】某同学利用如图甲所示的实验装置探究合力做功与动能变化之间的关系;
(1)实验中需要通过调整木板倾斜程度以平衡摩擦力,目的是______
A.为了使小车能做匀加速运动
B.为了增大绳子对小车的拉力
C.为了使绳子对小车做的功等于合外力对小车做的功
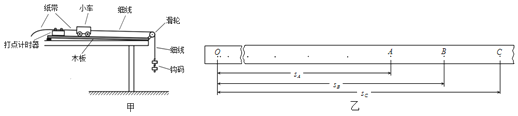
(3)为了使绳子的拉力约等于钩码的总重力,需要确保钩码的总质量远远小于小车的质量.实验时,先接通电源,再释放小车,得到图乙所示的一条纸带.在纸带上选取三个计数点A、B、C,测得它们到起始点O的距离分别为sA、sB、sC,相邻计数点间的时间间隔为T,已知当地重力加速度为g,实验时钩码的总质量为m,小车的质量为M.从O到B的运动过程中,拉力对小车做功W=________,小车动能变化量△Ek=__________
(4)另一位同学在本实验中,也平衡了摩擦力,并打出了一条纸带,但钩码的总质量m没有远远小于小车的质量M,在处理数据时,他仍然取绳子的拉力约等于钩码的总重力.该同学采用图象法进行数据分析:在纸带上选取多个计数点,测量起始点O到每个计数点的距离,并计算出每个计数点对应的小车速度v以及从O点到该计数点对应的过程中绳子拉力所做的功W,描绘出v2-W图象.请你根据所学的知识分析说明:该同学所描绘的v2-W图象应当是_________(填“直线”或“曲线”)(不考虑空气阻力影响).
【答案】 C mgsB ![]() 直线
直线
【解析】(1)实验前要把木板的一端适当垫高以平衡摩擦力,平衡摩擦力后小车受到的合力等于绳子的拉力,可以使绳子对小车做的功等于合外力对小车做的功,故AB错误,C正确;故选C.
(2)从O到B的运动过程中,拉力对小车做功W=mgsB;
打下B点时小车的速度: ![]() ,小车动能变化量△Ek=
,小车动能变化量△Ek=![]() Mv2=
Mv2=![]() ;
;
(4)设细线的拉力为F,小车发生位移为x时的速度大小为v,加速度大小为a,
根据牛顿第二定律,对于小车有:F=Ma①
对于钩码有:mg-F=ma②
本实验中:W=mgx③
根据匀变速运动学公式有:v2=2ax④
联立①②③④式可得:W=![]() (M+m)v2,v2=
(M+m)v2,v2=![]() W,
W,
由于M+m不变,则v2与W成正比,该同学所描绘的v2-W图象应当是直线.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】在探究小车的加速度a与小车质量M和小车受到的外力F的关系时,
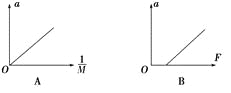
(1)探究加速度和力的关系的实验数据描绘出的a-F图象如图所示,下列说法正确的是________(填正确答案标号)。
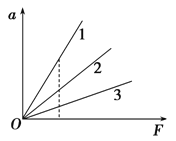
A.三条倾斜的直线所对应的小车的质量相等 |
B.三条倾斜的直线所对应的小车的质量不同 |
C.直线1所对应的小车的质量最大 |
D.直线3所对应的小车的质量最大 |
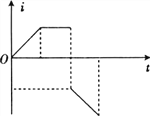
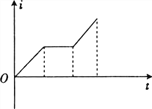
(2)由于没有始终满足小车的质量M远大于钩码的质量m的关系,结果得到的图象应是下图中的________(填正确答案标号)。