��Ŀ����
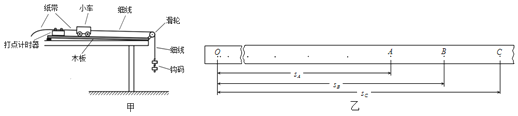
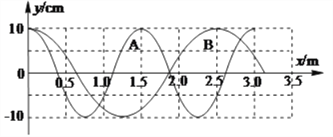
����Ŀ����ͼ����ʾ���⻬���㹻����ƽ�н�������MN��PQ�̶���ͬһˮƽ���ϣ���������L=0.3m�����������Բ��ƣ���������й̶�����R=0.4����������ͣ��һ����m=0.1kg������r=0.2���Ľ�����ab������װ�ô��ڴŸ�Ӧǿ��B=0.5T����ǿ�ų��У��ų�������ֱ���£�����һ����F��ˮƽ������������ab��ʹ֮�ɾ�ֹ��ʼ�˶����ȼ���ֱ���˶�����ѹ�������ɽ�R���˵ĵ�ѹU��ʱ�ɼ���������ԣ���õ�ѹU��ʱ��t�仯�Ĺ�ϵ��ͼ����ʾ��

��1��������˵�˲ʱ�ٶ���ʱ��仯�ı���ʽ��
��2�����2sĩ����F�Ĵ�С��
��3�����ˮƽ�����Ӿ�ֹ��������2s�����Ĺ�Ϊ1.2J����������·�в����Ľ������Ƕ��٣�
���𰸡���1��2t ��2��0.35N ��3��0.4J
����������1�����ݷ����ڵ�Ÿ�Ӧ���ɡ�ŷķ�����Ƶ���R���˵ĵ�ѹ���ٶȵĹ�ϵʽ���ɵ�ѹͼ��д����ѹ��ʱ��Ĺ�ϵʽ����������ٶȵı���ʽ�����ٶȵı���ʽ����������ٶȣ����ٶȹ�ʽ�����2sĩ���ٶȣ����������������ţ�ٵڶ������������������������ʹ�����˻�ö��ܡ���·�в������ܣ����������غ㶨�ɿ����������·�в����Ľ�������
��1����·�˵�ѹΪU���˵��˶��ٶ�Ϊv������
��Ӧ�綯��Ϊ��E=BLv ��Ӧ����Ϊ�� ![]() ���ݣ�U=IR
���ݣ�U=IR
�����ɵ��� ![]()
�������ݽ�ã� ![]()
��ͼ�ҿɵ���U=0.2t��V��
�ɵ��ٶ�Ϊ��v=2t��m/s��
��2������ʽv=2t֪�������˵ļ��ٶ�Ϊa=2m/s2����2sĩ�����˵��ٶ�Ϊ��v=at=4m/s��
��ʱ���ܵ��İ�������СΪ�� ![]()
��ţ�ٵڶ����ɣ��Ը���F��F��=ma
�������ݽ����F=0.35N
��3����2sĩ���˵Ķ���Ϊ�� ![]()
�������غ㶨�ɣ���·�����Ľ����� Q=W��Ek=0.4J