题目内容
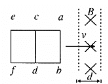
【题目】如图，两金属杆ab、cd的长度均为L=1m，电阻分别为Rab=0.2Ω、Rcd=0.8Ω，质量分别为mab=0.5kg、mcd=0.2kg，用两根质量及电阻均可忽略且不可伸长的柔软导线将两杆连接成闭合回路，悬挂在水平光滑绝缘圆棒两侧，两金属杆都保持水平，整个装置处在与回路平面垂直的匀强磁场中，匀强磁场磁感应强度B=0.5T，重力加速度g=10m／s2。释放两金属杆，经过一段时间后，金属杆以b匀速下落，不计导体棒间的安培力，求：
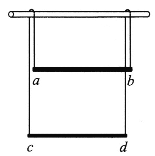
(1)金属杆ab匀速下落时，导线上的拉力大小；
(2)金属杆ab匀速下落的速度。
【答案】（1）1.75N（2）3m/s
【解析】
（1）导线上的拉力大小为FT，回路的电流为I，对ab棒：mabg=BIL+2FT；
对cd棒：2FT=BIL+mcdg
解得：FT=1.75N
（2）设金属杆ab匀速下落时回路中的感应电动势为E，则：E=2BLv
解得v=3m/s
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
