题目内容
10. 如图所示,在水平面和竖直墙壁之间放置质量为m、高为h的木块A和质量为M、半径为R的球B,各接触面均光滑,木块A受到水平向右的外力F作用,系统处于静止状态.O为B的球心,C为A、B接触点,CO与竖直方向夹角θ=60°.现撤去水平外力F,则( )
如图所示,在水平面和竖直墙壁之间放置质量为m、高为h的木块A和质量为M、半径为R的球B,各接触面均光滑,木块A受到水平向右的外力F作用,系统处于静止状态.O为B的球心,C为A、B接触点,CO与竖直方向夹角θ=60°.现撤去水平外力F,则( )| A. | 撤去外力F瞬间,木块A的加速度aA<$\frac{F}{m}$ | |
| B. | 撤去外力F瞬间,球B的加速度aB=0 | |
| C. | 撤去外力F瞬间,墙壁对球B的弹力FB=0 | |
| D. | 若球B着地前瞬间速度为υ,则此时木块速度为$\sqrt{\frac{M}{m}(2gh-gR-{υ^2})}$ |
分析 A和B原来处于平衡状态,当撤去F时,A、B原来的平衡状态就改变了,它们之间力的关系也随之改变,B球对A、对墙都要有作用力,可以判断B的加速度,球B着地前的瞬间速度,可以用机械能守恒来求解
解答 解:A、撤去F后,A、B之间力的关系也随之改变,因为对整体而言,墙壁的弹力是由形变产生的,撤去F,墙壁的弹力会发生变化,随之B对A的作用力也要发生变化,则A在水平方向上受到的合力比F要小,所以加速度也就小于$\frac{F}{m}$,故A正确;
B、撤去F后,A要向左运动,B要向下运动,A和B的运动状态都要发生变化,所以都要有加速度,即A和B的加速度都不是零,故B错误.
C、由于AB之间有力的作用,B要受到A的斜向上的力的作用,而B在水平方向上又不运动,所以墙对B一定要有力的作用,所以C错误.
D、对系统,根据机械能守恒定律可知:Mg(h+Rcosθ-R)=$\frac{1}{2}$Mv2+$\frac{1}{2}$mv′2
解得:木块速度v′=$\sqrt{\frac{M}{m}(2gh-gR-{υ}^{2})}$,所以D正确.
故选:AD
点评 撤去F后,A、B原来的平衡状态就改变了,它们之间的相互作用力不再是原来的力的大小,这是同学出错的地方,知道这一点这道题就可以了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.A、B、C是三个完全相同的金属小球,A、B位置固定,带有等量异种电荷,此时A、B之间的库仑力大小为F,用带有绝缘手柄的不带电的C球先后与A、B接触后将C移走A、B之间的库仑力大小变为( )
| A. | $\frac{1}{2}$F | B. | $\frac{1}{4}$F | C. | $\frac{1}{8}$F | D. | 0 |
1.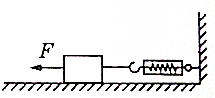 如图所示,当拉力F的大小为2N时,物体静止且弹簧测力计的示数为8N,则当拉力F大小变为12N时,弹簧测力计的示数为( )
如图所示,当拉力F的大小为2N时,物体静止且弹簧测力计的示数为8N,则当拉力F大小变为12N时,弹簧测力计的示数为( )
 如图所示,当拉力F的大小为2N时,物体静止且弹簧测力计的示数为8N,则当拉力F大小变为12N时,弹簧测力计的示数为( )
如图所示,当拉力F的大小为2N时,物体静止且弹簧测力计的示数为8N,则当拉力F大小变为12N时,弹簧测力计的示数为( )| A. | 12N | B. | 8N | C. | 4N | D. | 20N |
5.在某次十米跳台决赛中,一选手的质量为m,她沿竖直方向进入水后受水的阻力而做减速运动,设水对她的阻力大小恒为F,在水中下降高度h的过程中,下列说法正确的是( )
| A. | 重力势能减少了mgh | B. | 动能减少了Fh | ||
| C. | 机械能减少了Fh | D. | 机械能减少了(F-mg)h |
15.一辆卡车以15m/s的速度匀速行驶,司机突然发现正前方十字路口处有一个小孩跌倒在地,该司机刹车的反应时间为0.6s,刹车后卡车匀减速前进,最后停在小孩前1.5m处.已知刹车过程中卡车加速度的大小为5m/s2,则( )
| A. | 司机发现情况时,卡车与该小孩的距离为33m | |
| B. | 司机发现情况时,卡车与该小孩的距离为31.5 m | |
| C. | 司机发现情况后,卡车经过3.6s停下 | |
| D. | 司机发现情况后,卡车经过3s停下 |
19. 半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )
半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )
 半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )
半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )| A. | 第2s末粒子回到了原来位置 | |
| B. | 第3s内上极板为正极 | |
| C. | 第2s末两极板之间的电场强度大小为$\frac{π{r}^{2}}{10d}$(V/m) | |
| D. | t=3.4s时,下极板的电势为$\frac{π{r}^{2}}{20}$(V) |
 在实验操作前应该对实验进行适当的分析,研究平抛运动的实验装置如图所示,小球每次都从斜槽的同一位置无初速度释放,并从斜槽末端水平飞出.改变水平板的高度,就改变了小球在板上落点的位置,从而可描绘出小球的运动轨迹.某同学设想小球先后三次做平抛,将水平板依次放在如图1、2、3的位置,且1与2的间距等于2与3的间距.若三次实验中,小球从抛出点到落点的水平位移依次为x1、x2、x3,机械能的变化量依次为△E1、△E2、△E3,忽略空气阻力的影响,
在实验操作前应该对实验进行适当的分析,研究平抛运动的实验装置如图所示,小球每次都从斜槽的同一位置无初速度释放,并从斜槽末端水平飞出.改变水平板的高度,就改变了小球在板上落点的位置,从而可描绘出小球的运动轨迹.某同学设想小球先后三次做平抛,将水平板依次放在如图1、2、3的位置,且1与2的间距等于2与3的间距.若三次实验中,小球从抛出点到落点的水平位移依次为x1、x2、x3,机械能的变化量依次为△E1、△E2、△E3,忽略空气阻力的影响,
 如图,从距水平地面高h处以初速度v0水平抛出一质点,质点落地时速度方向与地面的夹角为α=45°,不计空气阻力,则:
如图,从距水平地面高h处以初速度v0水平抛出一质点,质点落地时速度方向与地面的夹角为α=45°,不计空气阻力,则: